ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 PEARSON Karl,
anglais, 1857-1936» Écart-type et variance | histogramme | coefficient de corrélation |
Mathématicien,
physicien, historien, Pearson eut Burnside, Cayley
et Stockes comme professeurs à l'université de
Cambridge. Il fut grandement
impressionné par son compatriote Francis Galton,
éminent savant,
physiologiste,
fondateur de l'eugénisme visant à
parfaire les caractères génétiques de l'espèce humaine.
Il sera d'ailleurs l'éditeur de Biometrika, fondé par
Galton, et à l'origine des Annals of Eugenics
(1925).
L'influence de ce dernier, qui fut tuteur de sa thèse (1879), le conduit finalement vers la statistique et il enseignera à l'University College de Londres après avoir poursuivi des études en sciences humaines en Allemagne (métaphysique, darwinisme).
Très importants travaux sur les distributions statistiques, la corrélation, les problèmes d'estimation sur échantillons pour lesquels il collabora avec Gosset, alias Student et Fisher (malgré des désaccords). Pearson est souvent considéré comme le fondateur de la statistique moderne. Son fils Egon Sharpe fut également statisticien.
Les notions de base de la statistique descriptive : »
| Loi de Pearson, également dite loi du χ2 (lire « khi 2 ») , test du χ2 : |
Introduite par Pearson en 1900, cette célèbre loi de probabilités fut en fait préalablement étudiée par l'astronome et géodésien allemand Friedrich Robert Helmert (1843-1917), auteur d'une Théorie mathématique et physique de géodésie supérieure (1880) dans le cadre de la théorie des erreurs. On la retrouve en fait plus avant encore sous la plume du français Bienaymé (bien connu pour la célèbre inégalité portant son nom) en application du théorème central limite appliquée à la loi multinomiale.
Son usage permet de confirmer ou infirmer avec un seuil de sûreté choisi par le statisticien (exprimé en termes de pourcentages), une hypothèse faite sur un phénomène aléatoire. La probabilité que χ2 soit inférieur à un réel α (seuil de probabilité) donné positif est :
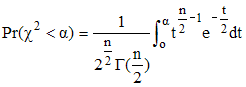
Étude de la loi de Pearson : » » Student
| On doit en outre à Pearson : |
♦ L'appellation
loi
normale pour désigner la seconde
loi de Laplace (voir
ici la 1ère) dans le cadre
de l'estimation des erreurs d'observation, également dite de
Laplace-Gauss ou
distribution gaussienne. Il s'agit de
"normal" au sens de "naturel".
Cette loi
de probabilité intervient dans de nombreux de
phénomènes quantitatifs aléatoires continus soumis à de
multiples causes (aucune d'entre elles n'étant prépondérante), agissant additivement et indépendamment l'une
de l'autre et dont la répartition des valeurs s'étale
autour de leur moyenne. Ce qui est le cas d'un grand nombre de phénomènes
naturels observables complexes (biologiques, sociologiques, astronomiques,
...).
Sur la page consacrée à Galton, on
constatera la volonté de la Nature et du Hasard (deux concepts intimement
liés) de guider des billes afin d'obtenir la célèbre
cloche de Gauss...
Dans une classe de niveau normal, il est n'est pas anormal
d'obtenir des diagrammes de notes rappelant la cloche de Gauss
(série unimodale), c'est à dire
la loi normale...
♦ Le terme de standard deviation (1893) pour signifier la racine carrée de la variance, ce que l'on appelle aujourd'hui l'écart-type ou l'écart quadratique moyen , à distinguer de l'écart moyen arithmétique peu pratique (» stat. élémentaires).
Cas des études statistiques à deux variables : » Cas d'une variable aléatoire continue : »
♦ La notion d'histogramme :
Un histogramme est une représentation graphique, au moyen de rectangles, d'une série de valeurs regroupées en classes (non nécessairement de même amplitude. On porte en abscisse l'amplitude des classes et l'aire d'un rectangle devra être proportionnelle à l'effectif des classes (où -ce qui revient au même- à la fréquence). Par suite, si les classes, n'ont pas toutes la même amplitude, à effectif égal, deux classes d'amplitudes différentes n'auront pas la même "hauteur" (ordonnée) alors qu'elles correspondent à un même pourcentage.
➔ Supposons une série regroupées en classes, pour laquelle [20,30[, d'amplitude 10 a même effectif que [70,90[ d'amplitude 20 : le rectangle de cette dernière sera deux fois "moins haut" que celui de la classe [20,30[ : à effectif égal, les aires doivent être les mêmes.
L'histogramme est à rapprocher du diagramme circulaire dont les angles des secteurs sont proportionnels aux effectifs (ou pourcentages, ou fréquences) des classes. Or l'aire d'un secteur est proportionnel à son angle. Ainsi dans un diagramme circulaire ou un histogramme, une surface deux fois plus importante (aire double) signifie une fréquence deux fois plus grande.
Ci-dessous, la classe [100,140[, d'amplitude 40, correspondant à 12% des effectifs est deux fois "moins haute" que la classe [20,40[, d'amplitude 20, de même fréquence (donc de même effectif), prise comme référence. La classe [140,200[, d'amplitude 60, correspondant à 6% des effectifs, est six fois "moins haute" que la classe de référence car 2 fois moins d'effectifs et 3 fois plus large.
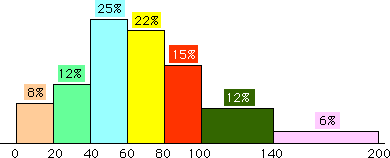
» voir l'exercice correspondant
D'une façon générale, si on note eff l'effectif d'une classe, freq sa fréquence, ampl son amplitude, u l'amplitude choisie comme référence (ci-dessus u = 20), alors, une unité graphique étant choisie, la hauteur h du rectangle associé est :
h = eff
× u/ampl ou, en termes de fréquence :
freq
× u/ampl
la "hauteur" h
d'un rectangle est inversement
proportionnelle à l'amplitude.
! Lorsque cela s'avère possible (faible disparité des données), on choisit d'utiliser des classes de même amplitude évitant des erreurs d'interprétation mais il ne faut cependant pas confondre diagramme en barres et histogramme : dans un diagramme en barres (pour des classes de même amplitude) ou en bâtons (série de valeurs), la hauteur de la barre (ou du bâton) est proportionnelle à l'effectif (voire égale, selon l'échelle utilisée) de la classe (ou de la valeur).
∗∗∗
Diagramme en barres,
médiane, classe modale , Diagramme circulaire
et histogramme,
Contrôle de vitesse
♦
Le
coefficient de corrélation :
Aussi
appelé coefficient de Bravais-Pearson,
ce paramètre a été préalablement
défini et utilisé par
Galton au tout début des années 1880 : si X et Y sont deux séries statistiques de n données
(xi,yi ) de type yi = f(xi),
de moyennes mx et my autrement dit
espérances
mathématiques E(X) et E(Y), de
variances respectives V(X) et V(Y), de
covariance cov(X,Y),
le coefficient de corrélation du couple (X,Y) est défini par :
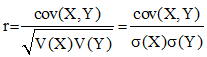
où σx et σy sont les écarts-types respectifs de X et Y, racines carrées de leur variance. Le coefficient de corrélation est compris entre -1 et 1 car cov2(X,Y) ≤ V(X)V(Y).
Lien avec le cosinus d'un angle dans un espace vectoriel normé de dimension finie : »
De plus,
si X' et Y' désignent les formes centrées et réduites de X et Y, à savoir :
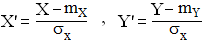
le coefficient de corrélation r est inchangé : cov(X',Y') = cov(X,Y) = r.
Compléments (étude statistique à deux variables) : »
♦ Interprétation du coefficient de corrélation :
Le coefficient de corrélation indique une présomption de liaison linéaire entre les deux séries d'autant qu'il sera proche de 1 en valeur absolue. Si r = ± 1, X et Y sont liés par une relation affine de type Y = aX + b. La justification du choix de ce coefficient r est donnée en complément sur la page relative à la méthode des moindres carrés.
Lorsque les phénomènes X et Y désignent des variables aléatoires indépendantes, le coefficient de corrélation r est nul car dans ce cas l'espérance du produit XY est le produit des espérances de X et de Y, ce qui annule la covariance. L'indépendance entre X et Y se détermine par un calcul sur les fréquences d'apparition des phénomènes X et Y (calcul des fréquences marginales).
! Inversement, un coefficient de corrélation faible, voire nul, ne signifie pas qu'il y a indépendance : la corrélation linéaire est un cas particulier de relation fonctionnelle entre deux variables aléatoires ou statistiques. On peut plus généralement chercher à approcher un nuage de point statistique par une courbe de type y = f(x) : on parle de régression, laquelle peut être linéaire, polynomial, logarithmique, exponentielle, etc.
Dans le cas de la méthode des moindres carrés, le minimum de la somme Δ des carrés des écarts par rapport à la droite de régression de y en x est égal à (1 - r2)V(Y), et à (1 - r2)V(X) par rapport à la droite de régression de x en y. En considérant la racine carrée (1 - r2)1/2σ(Y), on estime qu'une corrélation linéaire pertinente correspond à des écarts en ordonnée n'excédant pas, en valeur absolue, ½σ(Y), soit la moitié de l'écart-type des yi. Ce qui conduit à 1 - r2 < 1/4, soit r > √3/2 ≅ 0,87. Si | r | < 0,5, la présomption de linéarité est faible. Même conclusion relativement à la droite de régression de x en y.
Méthode des moindres carrés, corrélation linéaire, programme en ligne : »
∗∗∗
extrait BTS gestion 1990 | Exercice un peu tristounet... | Usure des pneus et puissance fiscale (couple pondéré) |
➔
Pour
en savoir plus :
Goursat