ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
» origine des termes : diagramme , histogramme » diagramme circulaire & histogramme... , statistiques perdues |
L'histogramme ci-dessous traduit les résultats obtenus en mathématiques dans un centre d'examen. En abscisse, on a porté les notes de 0 à 20, groupées par classes de même amplitude, et en ordonnée, les effectifs de chaque classe.
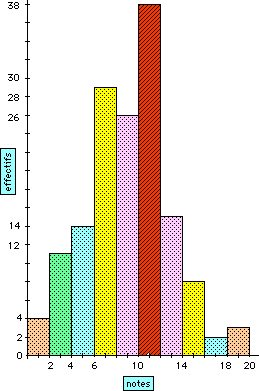
! Cet histogramme s'apparente à un diagramme en barres : les classes ayant même amplitude, les hauteurs des rectangles sont proportionnelles aux effectifs. Ce qui n'aurait pas lieu en cas d'amplitudes diverses, et l'indication des effectifs en ordonnée serait tout à fait illicite.
1. Etablir le tableau statistique comportant les éléments suivants :
- caractères
- effectifs
- effectifs cumulés croissants
- effectifs cumulés décroissants
2. Combien de candidats ont obtenu au moins la moyenne (soit au moins 10/20) ?
3. Quel est le pourcentage de candidats qui ont été éliminés (moins de 7/20) en admettant une répartition uniforme des notes dans chaque classe ?
4. Calculer la note moyenne et la note médiane. Préciser la classe modale (classe d'effectif maximal).
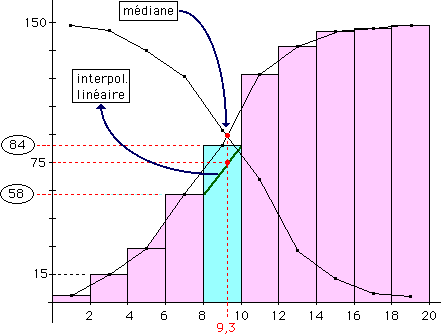
5. Construire les courbes des effectifs cumulés croissants et décroissants et vérifier graphiquement la valeur de la médiane calculée précédemment (interpolation linéaire).
Si vous séchez après avoir bien cherché : ››››
| Solution : |
1.
|
classes |
centres |
effectifs |
eff.
cumul. |
eff.
cumul. |
|
[0,2[ |
1 |
4 |
4 |
150 |
|
[2,4[ |
3 |
11 |
15 |
146 |
|
[4,6[ |
5 |
14 |
29 |
135 |
|
[6,8[ |
7 |
29 |
58 |
121 |
|
[8,10[ |
9 |
26 |
84 |
92 |
|
[10,12[ |
11 |
38 |
122 |
66 |
|
[12,14[ |
13 |
15 |
137 |
28 |
|
[14,16[ |
15 |
8 |
145 |
13 |
|
[16,18[ |
17 |
2 |
147 |
5 |
|
[18,20] |
19 |
3 |
150 |
3 |
2.
Il y avait 150 candidats. 150 - 84 = 66. Donc 66 candidats ont eu une note au moins égale à 10.
3.
4.
à 0,1 près, la note moyenne est 9,1.
La classe modale (celle d'effectif maximal) est la classe [10,12[.
La médiane correspond à la valeur du caractère pour laquelle il y a autant d'observations inférieures que supérieures. Cette valeur médiane partage l'histogramme des effectifs en deux parties de même aire. Ce sera ici la valeur de la 75ème note que l'on calcule en admettant une répartition uniforme des notes dans la classe médiane [8,10[ (interpolation linéaire) :
M = 8 + 2 × (75 - 58)/(84 - 58) ≅ 9,3.
» Notons que l'écart-type est 3,7. L'écart moyen arithmétique est 2,96
5.
La médiane s'interprète comme abscisse du point d'intersection des courbes des effectifs (ou des fréquences) cumulé(e)s croissant(e)s et décroissant(e)s. On la retrouve à l'intersection de l'horizontale d'ordonnée 75 (moitié de l'effectif de la population) et de la droite d'interpolation passant par les points d'entrée et sortie de la classe médiane.