ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 STOKES Sir George
Gabriel,
irlandais, 1819-1903 |
Savant éclectique, physicien, mathématicien,
philosophe, Stockes enseigna les mathématiques à l'université de Cambridge dès
1849 et y fut membre de la Société philosophique.
On lui doit une théorie de la fluorescence (1852) et une des premières théories ondulatoires de la lumière, indépendamment de Maxwell. Il étudia également la viscosité et les phénomènes de propagation des ondes de surface (comme le mouvement des vagues et leur déferlement) ainsi que celles du son. Il fut ainsi amené à étudier des champs scalaires ou vectoriels et les variétés différentiables (courbes de l'espace, surfaces, volumes) décrivant le système physique étudié.
En mécanique des fluides, il complète les travaux du français Claude Navier (polytechnicien, ingénieur des ponts & chaussées, 1785-1836, » réf.2) et les équations mises en place, dites de Navier-Stokes, sont encore aujourd'hui un sujet d'étude. Sans être invalidées, leur usage dans le champ d'applications à la mécanique contemporaine, aéronautique par exemple, demande une grande précision et leur résolution s'avère d'une grande complexité tant sur le plan mathématique. Raison pour laquelle elles font l'objet du 5è problème à "un million de dollars" posé en 2003 par le Clay Mathematics Institute.
Stokes fut élu à la Royal Society en 1851 et reçut la médaille Copley de la Royal Society en 1893, une distinction octroyée aux physiciens et biologistes (quoique parfois, par dérogation, à certains mathématiciens).
Formule de Stokes :
Cette formule permet de remplacer l'intégrale d'une forme différentielle P.dx + Q.dy + R.dz sur un arc de courbe rectifiable (c) par l'intégrale double sur une surface S non fermée et orientable de bord (c) :
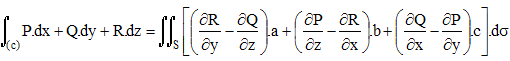
où a, b et c sont les coordonnées de la normale unitaire n à S orientée positivement et dσ un élément de surface.
i Si l'on se donne un champ vectoriel V de coordonnées (P,Q,R) dans une base orthonormale de l'espace, l'intégrande du second membre (sous le signe d'intégration) peut s'écrire rot V • n. » rotationnel
➔ Pour en savoir plus :
Puiseux