
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
Montant global du commerce extérieur et exportation construction automobile 1970-1979 » #1 , #2 , #4 , #5 (couple pondéré) |
» Source : extrait du sujet BTS Services Informatiques 1985
L'objectif de cet exercice est de rechercher une corrélation linéaire entre les séries chronologiques X et Y du commerce extérieur de la France et la part de sa production automobile à l'export durant les années 1970, exprimés en milliards de francs.
| Années | Série X : Commerce extérieur | Série Y : Production automobile à l'export |
| 1970 | 99,6 | 11.4 |
| 1971 | 114 | 13.6 |
| 1972 | 131.5 | 15.8 |
| 1973 | 159.7 | 18.2 |
| 1974 | 220.2 | 22.1 |
| 1975 | 223.3 | 27.3 |
| 1976 | 266.2 | 34.7 |
| 1977 | 311.5 | 42.2 |
| 1978 | 344.6 | 47.9 |
| 1979 | 416.9 | 55.9 |
1° Représenter le nuage de points associé à ce tableau (commerce extérieur en abscisse x et production automobile en ordonnée y). 1 cm pour pour 20 milliards de francs en x, 1 cm pour 2 milliards de francs. On placera l'origine en (80,10).
2°/ Calculer les valeurs exactes des coordonnées du point moyen.
3°/ Calculer les valeurs exactes des variances V(X) et V(Y) ainsi que celle de la covariance cov(X,Y)
4°/ Calculer le coefficient de corrélation linéaire à 10-2 près.
5°/ Déterminer les équations des droites de régression de y en x (D1) et de x en y (D2). On arrondira les coefficients à 10-3 près. Tracer ces droites dans le repère précédent. Conclure.
Si vous séchez après avoir bien cherché : ››››
| Solution : |
1°/ A l'exception du point (220.2,22.1), l'ensemble des points du nuage sont relativement bien alignés et une corrélation linéaire semble envisageable.
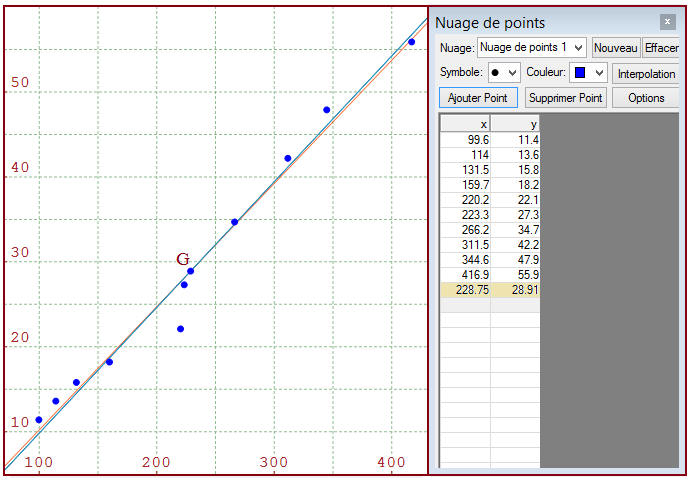
Le tableau statistique et l'ajustement vus par Graphmatica
2°/ Le point moyen est G(X,Y) = G(228.75,28.91).
3°/ La
variance V(X) est égale à la moyenne des carrés diminué du carré de la
moyenne, soit :
V(X) = 62451.289 - 52326.5625 = 10124.7265. De la même
manière, V(Y) = 217.5769.
La covariance
de X et Y est la moyenne des produit diminuée du produit des moyennes :
cov(X,Y) = 1469.4455.
4°/ σ(X) et σ(Y) désignant les écarts-types de X et de Y, racines carrées de leur variance, le coefficient de corrélation linéaire est le quotient r = cov(X,Y)/[σ(X) × σ(Y)] = 0.990079 ≅ 0.99.
| Point moyen : G(228.75,28.91) | Σxi = 2287.5 | Σyi = 289.1 | Σxi2 = 624512.89 |
| Σyi2 = 10533.65 | Σxiyi = 80826.08 | V(X) = 10124.7265 | σ(X) = 100.6217 |
| V(Y) = 217.5769 | σ(Y) = 14.750 | cov(X,Y) = 1469.4455 | r ≅ 0,99 |
5°/ La droite de régression de y en x a pour équation y - Y = a(x - X) avec a = cov(X,Y)/V(X) ≅ 0.145 :
D1 : y = 0.145x - 4.289
La droite de régression de x en y a pour équation x - X = a'(y - Y) avec a' = cov(X,Y)/V(Y) ≅ 6.754 :
D2 : x = 6.754y + 33.501
On constate que les deux droites sont "quasiment" identiques dans le champ [100,400] x [10,60]. Rien d'étonnant puisque r2 = aa' ≅ 1 et, ramenée à y en fonction de x, D2 a pour équation y = 0.148x - 4.96, qui est sensiblement celle de D1. Une corrélation linéaire apparaît pertinente et signifie que la construction automobile destinée à l'export varie avec un taux constant dans le même sens (pentes > 0) que le chiffre du commerce extérieur.
Paramètres obtenus au moyen du programme des moindres carrés :
