ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 KÖNIG
(ou
KOENIG) Samuel,
allemand, 1712-1757 |
Physicien, philosophe,
juriste. Ami de Voltaire, il fut l'élève de
Jean
Bernoulli, du baron
de Wolf et de Leibniz.
Il enseigna les mathématiques, la philosophie et le droit à La Haye. Ses recherches portent en mécanique, et en calcul des
probabilités.
König fut un adversaire acharné de Maupertuis à propos de son principe de moindre action qu'il attribuait à Leibniz.
En physique, un repère de König est synonyme de repère barycentrique : c'est à dire dont l'origine est le centre de gravité d'un système en mouvement de translation par rapport à un système galiléen (du nom de Galilée).
En mathématiques, on rencontre son nom dans les cours de
probabilités, souvent jumelé à Huygens, pour le
calcul de la variance d'une série statistique :
| Formules dites de König pour la variance et la covariance (cas discret) : |
Si X désigne une variable aléatoire discrète ou une série de données statistiques sa variance est la moyenne (espérance mathématique) des carrés des écarts à la moyenne x = E(X), c'est à dire :
V(X) = E(X - x )2
En termes de série statistique x1, x2, ..., xN , ni désignant l'effectif partiel de la donnée xi, la formule s'écrit :
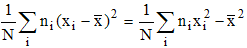
Également attribuée à Huygens qui l'utilisa 80 ans plus tôt dans des données d'observation astronomique, la formule de König pour la variance est extrêmement utile dans la pratique :
V(X) = E(X2) - [E(X)]2
Preuve : Les propriétés de linéarité de l'espérance mathématique permettent d'écrire V(X) = E(X - x)2 = E(X2) - E(2xX) + E(x2) = E(X2) - 2xE(X) + x2 = E(X2) - 2x2 +x2 = E(X2) - x2 = E(X2) - [E(X)]2.
∗∗∗
Étude d'un tableau statistique #1
Tableau statistique à deux variables X et Y :
La covariance entre deux variables aléatoires ou séries statistiques X et Y, de moyennes respectives x et y, est la moyenne du produit des variables centrés X - x et Y - y, à savoir :
cov(X,Y) = E[(X - x )(Y - y)]
Dans le cas élémentaire d'une série statistique double (x1, y1), (x2, y2), ..., xN, yN), la formule s'écrit :
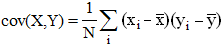cas plus général d'un couple statistique :
»
La formule de König pour la covariance est alors :
cov(X,Y) = E(XY) - E(X)E(Y) =
XY
-
X ×
Y
espérance du produit diminué du produit
des espérances
Preuve : Les propriétés de linéarité de l'espérance mathématique permettent d'écrire cov(XY) = E(XY) - y × E(X) - x × E(Y) + x × y. Les deux derniers termes s'annulent et le résultat annoncé est confirmé.
Corrélation linéaire et méthode des moindres carrés : »
Remarque :
La covariance est une forme bilinéaire symétrique dont la forme quadratique associée est la variance : cov(X,X) = V(X).
Cas d'une variable aléatoire continue :
»
»
Huygens , Pearson
Clairaut