
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|
! Le but de cette étude est de constater que des résultats statistiques portant sur une certaine période et possédant des propriétés remarquables (comme ici un ajustement linéaire tout à fait justifié) ne peuvent être extrapolés sans précaution.
L' Annuaire statistique de la France donne le tableau suivant indiquant le taux pour mille (‰) de mortalité infantile par période quinquennales de 1886 à 1940 :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
➔
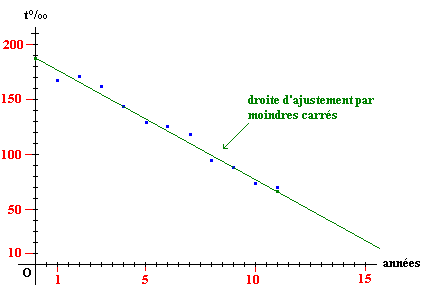
le taux de mortalité infantile est un indice exprimant le nombre de décès pour 1000 naissances sur une période de 1 an.1. Représenter graphiquement les données précédentes par un nuage (ensemble de points non reliés) de 11 points. On prendra comme abscisse 1,2,...11 : 1 sera l'année 1888, 2 l'année 1893, ... , 11 l'année 1938.

2. Vous constatez que les points sont susceptibles d'être ajustés linéairement. Calculer le coefficient de corrélation et procédez à l'ajustement par la méthode des moindres carrés.
3. Montrer que l'abscisse n d'une année An > 1887 est donnée par : An - 1888 = 5(n - 1).
Quelle est l'abscisse de l'année 1988 ? Quel serait le taux en admettant que la droite d'ajustement trouvée est encore valable ?
Si vous séchez après avoir bien cherché : ››››
| Solution : |
1°/
2°/ Le coefficient de corrélation linéaire est donné par la formule :
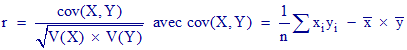
Le tableau ci-dessous résume les différents
paramètres statistiques (V = variance, σ
= écart-type) des séries observées.
| r | = 0,989 est proche de 1 : forte
présomption d'alignement. La droite de régression de y en x (ajustement linéaire) par
la méthode des moindres carrés a
sensiblement pour équation :
y = -11x + 187.
| Point moyen : G(6,122) | Σxi = 66 | Σyi = 1342 | Σxi2 = 506 |
| Σyi2 = 177062 | Σxiyi = 6854 | V(xi) = 10 | σ(xi) = 3,1623 |
| V(yi) = 1212,546 | σ(yi) = 34,8216 | cov(xi,yi) = -108,9091 | r = - 0,989 |
➔ Rappelons que si (d) : y = ax + b est l'équation de la droite de régression de y en x, le coefficient directeur de cette droite est donné par la formule : a = cov(X,Y)/V(X); l'ordonnée à l'origine se calcule facilement sachant que (d) passe par le point moyen G(Σxi,Σyi).
» programme JavaScript en line
3°/ Les classes ont une amplitude de 5 ans; si 1888, centre de la classe, correspond à l'abscisse n = 1, les années sont en progression arithmétique (An) de raison 5, de 1er terme 1888; on a donc : An = 1888 + (n - 1) × 5, ou encore :
An - 1888 = 5(n - 1)
! On constate qu'une prédiction à long terme (x = 21 : 100 ans entre 1888 et 1988) n'a pas de sens : le taux serait négatif ! Toute extrapolation de résultats statistiques doit bien sûr tenir compte de changements significatifs dans une population donnée.
➔ Dans la première moitié du 20e siècle les progrès de la médecine, dus pour beaucoup à Pasteur (1822-1895), ont permis d'éradiquer un grand nombre de maladies du nourrisson.
De plus, en Europe en particulier, les naissances ont lieu désormais dans des maternités avec un suivi de l'enfant, ce qui n'était pas le cas jusque dans les années 1950. La mortalité infantile a beaucoup baissé depuis cette époque mais cette évolution est plus lente. En France, le taux était de 7,8‰ en 1988; 4,2 en 2002; 3,4 en 2008.

» On pourra consulter de nombreuses statistiques sur http://www.indexmundi.com/