ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

 De son vrai nom
Gosset, ce statisticien fit ses études au College de
Winchester et au New College d'Oxford. Cadre durant toute sa carrière
à la brasserie Arthur Guinness de 1899 à 1935, Gosset
fut initialement
embauché à Dublin, puis nommé à Londres en 1905 afin de diriger
une nouvelle brasserie, tout en étant chargé d'études statistiques pour le compte
de la société.
De son vrai nom
Gosset, ce statisticien fit ses études au College de
Winchester et au New College d'Oxford. Cadre durant toute sa carrière
à la brasserie Arthur Guinness de 1899 à 1935, Gosset
fut initialement
embauché à Dublin, puis nommé à Londres en 1905 afin de diriger
une nouvelle brasserie, tout en étant chargé d'études statistiques pour le compte
de la société.
C'est ainsi qu'il rencontra son compatriote Karl Pearson à l'University College de Londres. On lui doit d'importants résultats sur la théorie de l'estimation. C'est sous son nom d'emprunt que Gosset publiera tous les résultats issus de ses recherches en matière de statistiques.
La loi t évoquée ci-dessous, t comme test, porte son nom. Basée sur celle de Pearson (dite du χ2, prononcer khi 2), elle est utilisée afin de confirmer ou rejeter des hypothèses relatives aux paramètres observés d'une loi (espérance mathématique en particulier) :
|
Loi de Student (loi t), également dite de Student-Fisher (1908) : |
Il s'agit de la loi de probabilités suivie par la variable aléatoire :
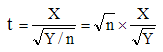
où X et Y désignent des variables aléatoires indépendantes, X suivant une loi gaussienne réduite et Y une loi du χ2 à n degrés de liberté.
Γ désignant la fonction « gamma » de Euler, la densité de cette loi est exprimée par :
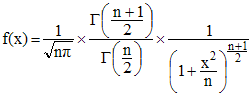
On dit, comme pour la loi du du χ2, que n est le nombre de degrés de libertés. L'espérance mathématique de t est nulle pour n > 1, sa variance est n/(n - 2), n ≠ 2
∗∗∗
Étudier les cas n
= 1 et n = 2.
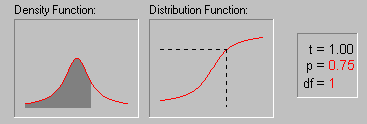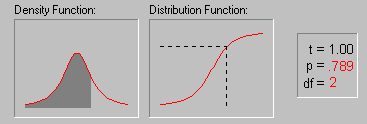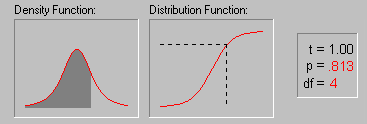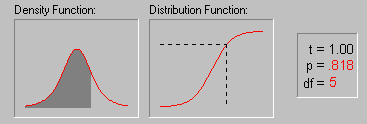
La représentation de f est une courbe en cloche et on peut montrer que la forme limite de cette loi est la loi normale centrée réduite (illustration empruntée avec l'aimable autorisation du site indiqué ci-dessous) :
© Copyright
StatSoft, Inc., 1984-2005
df désigne ici le nombre de degrés de liberté (degree of
freedom)
La loi de Cauchy, également appelée loi de Lorentz, du nom du célèbre physicien hollandais Hendrik Antoon Lorentz (1853-1928), est une loi de Student à 1 degré de liberté. En effet, sa densité est :
![]()
et correspond à n = 1 dans la densité de la loi de Student car Γ(1) = 1 et Γ(1/2) = √π.
»
Fisher Loi de Pearson, dite du χ2
: »
➔ Pour en savoir plus :