
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|
Regarde bien cette figure géométrique :
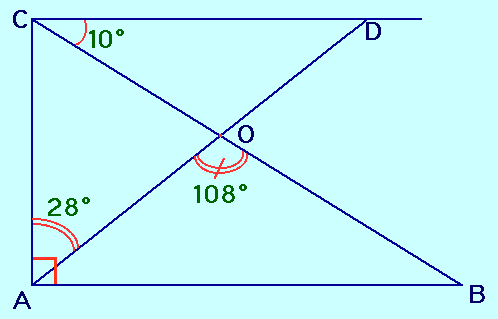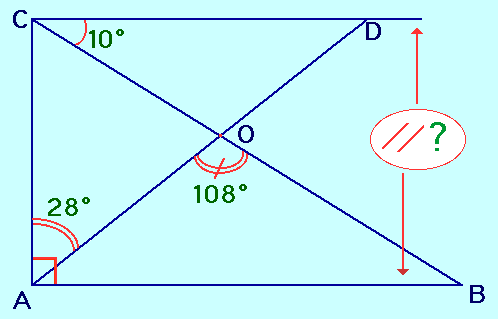
Elle est volontairement fausse; on voit bien que les mesures des angles ne sont pas respectées, tu dois bien observer le codage et répondre à cette question :
Les droites (AB) et (CD) sont-elles "vraiment" parallèles ?
Complète :
Les droites (CD) et (AB)
déterminent sur la sécante (.....) des angles ...............-............. de même mesure,
à savoir ^ABO et ^DCO.
Ces droites sont donc
effectivement ....................
ou bien (autre méthode de raisonnement) :
Le triangle ABC étant ................ en A, les droites (CD) et (AB) sont toutes deux ......................... à (AC); ces droites sont donc effectivement .....................
| Solution #1 : |
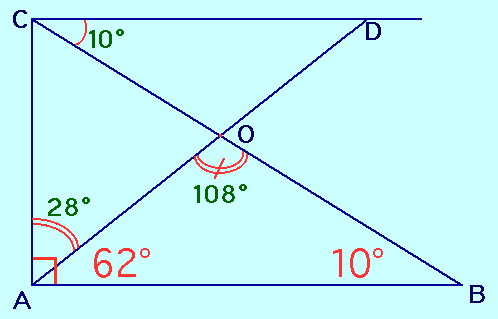
ou bien :
^ACO = 180° - 72° - 28° = 80°