
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

 |
» rappel de cours » #1 , #3 , #4 , #5 , #6 , #7 |
Regarde bien la figure animée ci-dessous :
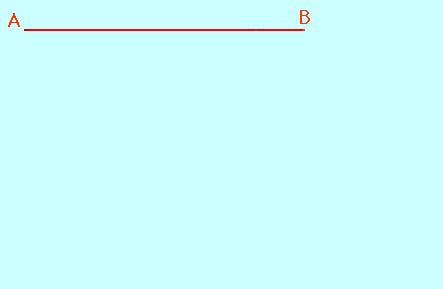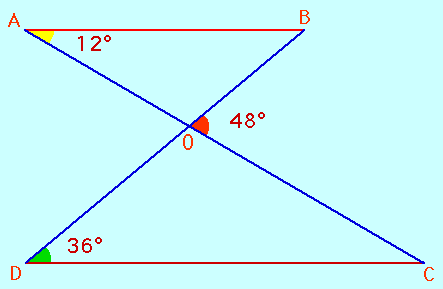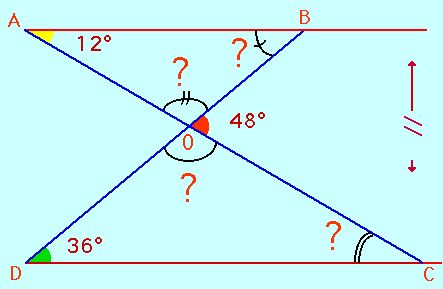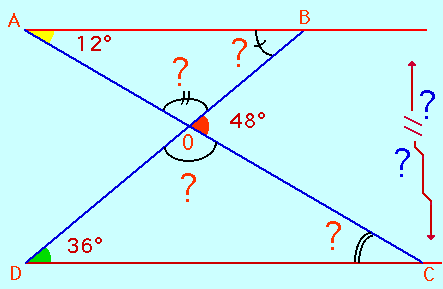
Tu as sans doute bien compris le problème. On précise que les points A, O, C d'une part et B, O, D d'autre part sont alignés. Quant au reste, ne te fies pas au dessin qui est volontairement faux.
|
Solution #2 : |
Il s'agit de calculer les angles marqués d'un point d'interrogation et de dire si les droites (AB) et (CD) sont parallèles ou non.
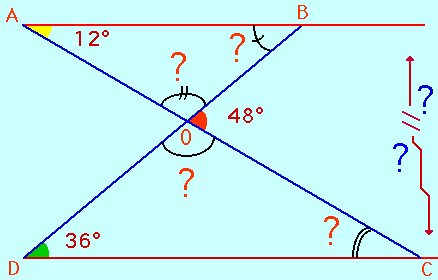
♦
L'angle ^BOD est plat
donc ^DOC = 180° - ........° = 132°.
^AOB mesure également
132° car il est opposé à ^DOC (angles ............... par
le s..........t).
♦ La somme des angles d'un triangle égale
........°.
Par conséquent,
dans le triangle DOC, on a ^DCO = 180° - ........ - ......... ° = 12°.
♦
On peut donc écrire ^DOC = ^DCA = ^BAC = 12°. Les angles ^BAC et ^DCA,
formés par les droites (AB) et (CD) coupées par la sécante (AC), sont en situation
a...........s-i...........s.
Ces angles étant ...........,
on peut affirmer que les droites (AB) et (CD) sont ................ .
♦
Quant à ^ABD, puisque nous savons maintenant que (AB) et (CD) sont
..............., il mesure 36° comme ^CDB puisque ces angles sont en situation
............................ par
rapport à la sécante (.....).