ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Observer, démontrer : angles et parallèles #7      niveau 5è           » cours    » #1 , #2 , #3 , #4 , #5 , #6

Voici une figure géométrique :

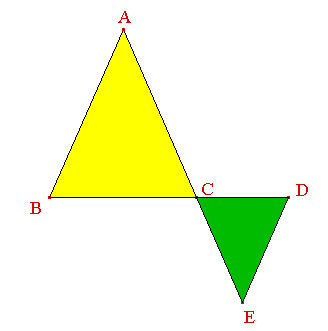
La même figure générée au moyen du logiciel de géométrie dynamique Cabri Géomètre, dans sa version CabriJava pour Internet :

Si ton navigateur accepte les applets Java (avec CheerpJ) :
Tu  peux déplacer les points A, C et D

• Sachant que les triangles ABC et CDE sont isocèles en A et E respectivement, code la figure et

Prouve que les droites (AB) et (DE) sont parallèles.

• Par hypothèse, ABC est isocèle en A, donc AB = AC et  ^ABC = ^ACB;

• Par hypothèse, CDE est isocèle en E, donc EC = ED et  ^ECD = ^EDC;

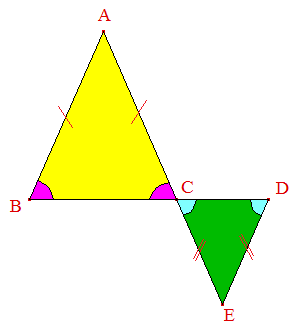
• Les angles ^ACB et ^ECD sont opposés par le sommet : ils ont donc même mesure;

• Par suite : ^EDC = ^ABC.

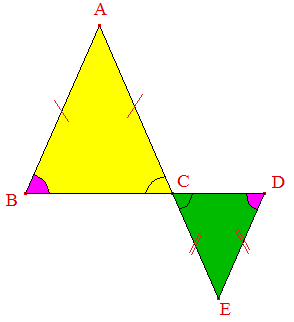
En conséquence, la sécante (AE) détermine sur les droites (AB) et (DE) des angles alternes-internes de même mesure :

(AB) et (DE) sont donc parallèles

Si ton navigateur accepte les applets Java (avec CheerpJ) :
Tu  peux déplacer les points A, C et D
 

 ➔   Remarquer qu'en "tirant" C vers la droite, les deux triangles ABC et CDE sont d'un même côté par rapport à (BD); il s'agit alors de comparer des angles correspondants et non plus alternes-internes.