ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

apprendre à rédiger : angles et parallèles #6      niveau 5è    cours    » #1 , #2 , #3 , #4 , #5 , #7

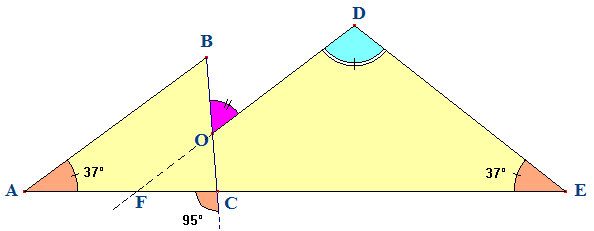
Question :        

Sachant que (AB) est parallèle à la droite (OD), calculer les mesures des angles ^BOD et ^ODE ?

Réponse à compléter :         

• Dans le triangle ABC, on a ^BCA = ......... - 95° = ............°.
  
  Dans un triangle la  ............. des mesures des angles est égale à  .........°.
  
  Par conséquent ^ABC = 180° - ........ - ........ = 58°.
  

• Par hypothèse, on a (AB)........(OD). Ces droites forment donc, avec la sécante (.........), des angles
  alternes-............... de même mesure : ^ABC = ^.............
  

• En conclusion  : ^BOD = 58°.

• Pour calculer ^ODE, on peut considérer le quadrilatère ODEC dont la somme des angles est .........°
  et remarquer que ^OCE = 95° et ^DOC = 180 -  ....... = ........°.
  

• En conclusion : ^ODE = 360 - (95 - ........ - 37) = 106°

Mais il est intéressant de constater ici qu'en compliquant la figure, on simplifie la solution... :

• Prolongeons [DO) coupant [AC] en F (tracé en pointillés) : on obtient un angle ^DFE = 37° car les parallèles (AB) et (OD) forment avec la sécante (AE) des angles ......................... de même mesure. 

• Dans le triangle FDE, on a alors  :

^FDE = ^ODE = 180° - 2 x .......° = 106°