ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Observer, construire, démontrer : angles et parallèles #3           niveau 5è    »  rappel de cours    » #1 , #2 , #4 , #5 , #6 , #7

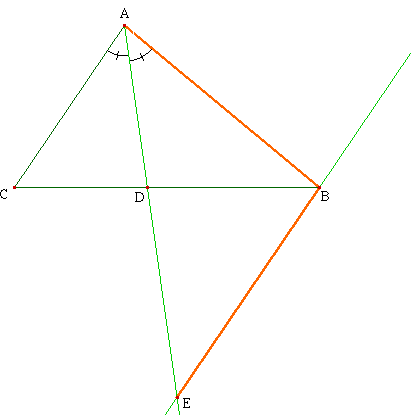
• 1 - Sachant que le côté [AC] du triangle ABC est parallèle à la droite (BE),
       pourrais-tu reconstituer le programme de construction de cette figure géométrique ?

• 2 - Que pourrait-on être amené à démontrer ?

• 3 - Si tu as émis une conjecture (une réponse à la question 2 et que tu crois juste),
       pourrais-tu la prouver ?           

1-  Enoncé (programme de construction) :

• Tracer un triangle (quelconque) ABC;

• La bissectrice de l'angle ^CAB coupe le côté [BC] en D.

• La parallèle à (AC) passant par B coupe (AD) en E.

2-  Le triangle ABE semble isocèle. La question est alors :

Prouver que le triangle ABE est isocèle, de sommet principal B.

3- Les droites parallèles (AC) et (BE) forment, avec la sécante (AE), des angles alternes-internes de même mesure; par conséquent :

^CAE = ^AEB.

Mais [AE) est la bissectrice de l'angle ^CAB; donc :

^CAE = ^BAE

On en déduit l'égalité : ^BAE = ^AEB. C'est bien dire que le triangle ABE est isocèle de sommet principal B.