
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
» cours » #1 , #2 , #3 , #4 , #6 , #7 |
1 -
Construis, au moyen
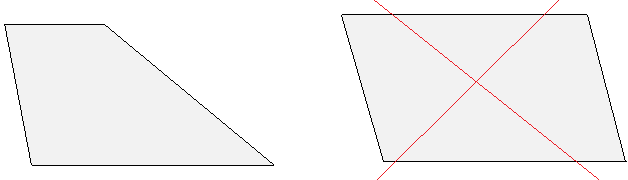
de la règle (non graduée) et du compas, un trapèze ABCD de bases [AB] et [CD] et tel que CB = CD.
 On devra construire un vrai
trapèze, au
sens strict : il ne doit pas être un parallélogramme
! Il doit ressembler à la figure de gauche :
On devra construire un vrai
trapèze, au
sens strict : il ne doit pas être un parallélogramme
! Il doit ressembler à la figure de gauche :
» Rappel : construction géométrique au sens d'Euclide i vérifier ta construction
2 -
Démontre maintenant que [BD)
est la bissectrice de l'angle ^ABC.
Si tu sèches après avoir bien cherché : ››››
» N.B. Cet exercice est honteusement inspiré d'un très bon livre de 5è, Collection Cinq sur Cinq - Ed. Hachette - 1997
| Solution : |
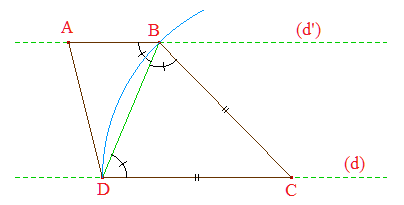
1. Construction :

Tracer une droite (d);
Tracer une droite (d') parallèle à (d)
Soit [DC] un segment de (d);
Le cercle de
centre C passant par D coupe (d') en B;
Si
l'arc de cercle ne coupe pas (d'), on devra changer le point D :
CD doit être supérieur à la distance
entre (d)
et (d')
Choisir un point A sur (d') de sorte que le quadrilatère ABCD soit non croisé;
Tracer
[AD]; [AB] et [BC].
Éviter
que ABCD soit un parallélogramme : cas particulier pour les
uns, erreur pour d'autres si l'on prend comme définition du
trapèze : quadrilatère ayant une seule paire de
côtés parallèles.
2. [BD) est la bissectrice de l'angle ^ABC :
Par hypothèse,
CD = CB, le triangle BCD est donc isocèle,
de sommet principal C.
C'est dire que ^DBC = ^BDC.
Par hypothèse ABCD est un
trapèze de bases [AB] et [CD]
C'est dire que les droites (AB) et (CD) sont
parallèles.
Les angles
alternes-internes
^ABD et
^BDC définis par les droites parallèles (AB) et (CD)
et
la sécante (BD) ont donc même mesure.
Ainsi ^DBC = ^BDC et ^ABD = ^BDC.
En conséquence : ^DBC = ^ABD, ce qui prouve que
[BD) est la bissectrice de l'angle ^ABC.