
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

» Norme et espace vectoriel normé | Normes et distances équivalentes | Espace et algèbre de Banach | Théorèmes |
 i
Source
éléments
biographiques : CDSB
&
Encyclopædia
Britannica.
i
Source
éléments
biographiques : CDSB
&
Encyclopædia
Britannica.
Portrait :
PTM (Polskie Towarzystwo
Matematyczne)
Confié par son père à une famille d'accueil de Cracovie, proche de la maison familiale, le jeune Stephan porte le nom de sa mère qu'il ne connut pas. Après des études secondaires en cette ville, Banach étudia à l'École Polytechnique de Lvov (on disait Lviv à l'époque), ville de l'actuelle Ukraine, jusqu'en 1914. C'est alors qu'éclate la première guerre mondiale. Réformé pour défaut de vision, Banach revient à Cracovie où, embauché comme ingénieur dans la construction des routes, il poursuit des recherches mathématiques tout en donnant des cours particuliers.
En 1919, à l'issue de la guerre, il regagne Lvov et soutient une thèse de doctorat Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales (1920) dirigée par Steinhaus qui deviendra son ami (ce dernier est son aîné de seulement 5 ans).
La thèse de Banach contenait déjà, indépendamment de l'américain Wiener à la même époque, la définition formelle des espace vectoriels normés. Il obtint une chaire à l'université de Lvov en 1922 et y enseigna durant toute sa carrière (il en fut le doyen en 1940-41), décédant prématurément d'un cancer du poumon en 1945 alors qu'il devait obtenir un poste à l'université Jagellonne de Cracovie.
Banach créa, avec son compatriote et ami d'études H. Steinhaus, la revue Studia Mathematica (1929)qui fit la renommée de l'université de Lvov et permit le rayonnement de la mathématique polonaise en Europe. En 1932, Banach publia son plus remarquable ouvrage : Théorie des opérations linéaires, amenant rigueur et résultats novateurs en analyse fonctionnelle, qui sera 40 années durant la référence en la matière.
Quelques précisions historiques :
Cracovie est l'ancienne capitale de la Pologne. Fondée vers le 8è siècle sur les rives de la Vistule par un chef slave nommé Krakus. C'est en 1609 que le roi Sigismond III établit sa capitale à Varsovie. Devenue autrichienne en 1846, Cracovie redevient polonaise en 1918. Créée en 1364, son université Jagellonne, du nom d'une ancienne dynastie royale, est avec celle de Prague (fondée en 1348) la plus ancienne d'Europe centrale. Créée en 1815, la Société scientifique de Cracovie fut une société savante très féconde. Zlle devint académie des sciences de Cracovie en 1873.
La vie scientifique à Cracovie au XIXè siècle :
http://www.persee.fr/web/revues/home/prescript/article/rhs_0048-7996_1968_num_21_2_2555...
Lvov fut, et est encore, une ville universitaire renommée : polonaise dès 1349, elle devient autrichienne en 1772 et sera la capitale de la province de Galicie. Tout comme Cracovie, à l'issue de la 1ère guerre mondiale, Lvov est rendue à la Pologne. Mais, disputée entre russes et allemands, elle deviendra ukrainienne (au sein de l'ex URSS) après la seconde seconde guerre mondiale.
| Norme, semi-norme, espaces vectoriels normés : |
Dans un espace vectoriel E sur un corps commutatif K = R ou C, une norme est une application de E dans K qui à tout vecteur u associe le nombre généralement noté || u || vérifiant :
La propriété 2 est appelée inégalité triangulaire par analogie avec le cas concret des vecteurs du plan. La norme est à l'espace vectoriel ce que la distance est à l'espace métrique, notion introduite par Fréchet (1906) que Hausdorff développera magistralement dans un contexte topologique (Mengenlehre, 1913).
Fréchet et l'introduction des espaces métriques : »
➔ On parle de semi-norme si l'axiome 1 ci-dessus n'est pas valide. On notera toutefois que l'axiome 3 implique || 0E || = 0 et on vérifiera sans peine que si E est de dimension 1, toute semi-norme est une norme.
∗∗∗
a) Vérifier que dans
C2 = C × C,
l'application qui à tout couple (z,z') associe | z | est une semi-norme.
Que peut-on dire de (z,z')
→ | z
| + | z' | ?
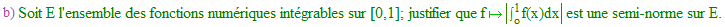
Deux cas importants où interviennent les semi-normes dans les espaces fonctionnels :
Topologie engendrée par une famille de demi-normes : » Espaces Lp : »
∗∗∗
Exemples usuels d'espaces normés :
♦ R en tant qu'espace vectoriel sur lui-même muni de la valeur absolue est un espace vectoriel normé.
♦ Dans le plan vectoriel euclidien, la norme d'un vecteur AB n'est autre que la distance séparant A de B. Cette norme peut être définie par le produit scalaire usuel, dit euclidien, de deux vecteurs. Il en est de même dans l'espace vectoriel euclidien de dimension 3, rapporté à un repère "orthonormé" (ou identifié à l'espace vectoriel R3) muni du produit scalaire usuel , noté ci-dessous • :
♦ Si l'on considère l'espace vectoriel E des fonctions numériques définies et continues sur un intervalle [a,b] de R, on peut définir une norme sur E par :
Un espace vectoriel peut être muni de plusieurs normes : on peut définir sur E une autre norme en associant à toute fonction f, le nombre :
![]() »
Hilbert
»
Hilbert
➔ Si f n'est pas continue mais seulement intégrable sur [a,b], on n'a plus une norme mais une semi-norme !
♦ Soit E un ensemble (non vide) et F est un espace vectoriel normé dont la norme est notée || ||F. On peut munir l'ensemble des fonctions bornées de E vers F de la norme :
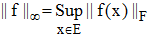
appelée norme de la convergence uniforme. Elle se rencontre en effet dans la définition d'une suite de fonctions uniformément convergente :
Weierstrass et la convergence uniforme : »
| Normes et distances équivalentes : |
Une norme || ||2 sur un espace vectoriel réel E est dite équivalente à une norme || ||1 définie sur ce même espace, s'il existe des réels a et b tels que pour tout x de E, on ait :
a|| x ||1 ≤ || x ||2 ≤ b|| x ||1
➔ On a une définition semblable pour des distances équivalentes dans un espace métrique. Pour un tel espace de distance d :
a × d1(x,y) ≤ d2(x,y) ≤ b × d1(x,y)
On définit ainsi une relation d'équivalence entre normes définies sur E. Dans un espace vectoriel réel de dimension finie, toutes les normes sont équivalentes. Si une convergence a lieu relativement à une norme, elle aura lieu dans les mêmes conditions (uniforme, par exemple) pour toute autre norme équivalente. L'intérêt de cette notion est de pouvoir simplifier des calculs en utilisant une norme plus "opérationnelle".
Des exemples classiques :
Dans l'espace R3 ou par généralisation évidente, dans Rn, les normes suivantes sont équivalentes :
Dans l'espace Mn(R) des matrices carrées à termes réels :
;
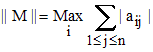
norme spectrale : les λ sont les valeurs propres de tM×M. » Hermite
| Espace de Banach, Algèbre de Banach : |
 On appelle espace de Banach un espace
vectoriel normé et complet
: dans un tel espace E, toute suite
de Cauchy est convergente dans E. Rappelons
ici que :
On appelle espace de Banach un espace
vectoriel normé et complet
: dans un tel espace E, toute suite
de Cauchy est convergente dans E. Rappelons
ici que :
Tout espace vectoriel sur R normé et de dimension finie est complet.
L'ensemble C des nombres complexes, en tant qu'espace vectoriel de dimension 2 sur R, de base (1,i) peut être considéré comme un espace Banach en posant et || z || = | z |, norme de z.
Muni du produit de convolution, considéré comme multiplication, l'espace L1 des fonctions numériques intégrables sur R est un espace de Banach.
L'inégalité triangulaire porte sur la norme de la somme de deux vecteurs. Dans le cas d'une algèbre normée, on peut aussi imposer une contrainte sur le produit :
Une algèbre de Banach est une algèbre A sur C dont l'espace vectoriel associé est un espace de Banach et vérifiant en outre pour tout couple (x,y) d'éléments l'inégalité :
|| u × v || ≤ || u ||.|| v ||
où " × " désigne la multiplication dans A et "." la multiplication usuelle de C (de R+ dans le cas présent).
∗∗∗
Vérifier que si E désigne un ensemble non vide,
l'ensemble F des fonctions bornées de E dans C muni
de la norme || f ||∞ de
la convergence uniforme, est une algèbre de
Banach.
» Algèbre de Wiener | Riesz et les espaces Lp | Espaces de Hilbert | Fréchet et les espace métriques
| Un théorème de Banach : |
E et F désignent deux espaces de Banach :
Si f une application linéaire bijective (isomorphisme) et continue de E dans F, alors f-1 est un isomorphisme continu de f dans E.
| Théorème de Hahn-Banach : |
Ce théorème, valable en dimension infinie grâce à l'axiome de Zorn, peut ainsi s'exprimer :
Dans un espace de Banach, toute forme linéaire continue sur un sous-espace est prolongeable à l'espace tout entier.
Les conséquences de ce théorème sont très importantes en analyse fonctionnelle et en topologie (espaces convexes, théorèmes de séparation).
» Hahn Continuité et applications linéaires : »
| Théorème de Banach-Steinhaus : |
Il s'agit d'un important théorème sur la convergence d'applications linéaires continues :
| Théorème du point fixe de Banach pour les fonctions contractantes : |
E désigne un espace de Banach et f est une application de E dans E telle qu'il existe un réel k de l'intervalle ]0,1[ pour lequel :
∀(x,y)∈E2, ||f(x) - f(y)|| ≤ k.||x - y|| » Lipschitz , Steinhaus
(on dit que f est contractante). Dans ces conditions f admet un unique point invariant u : f(u) = u, obtenu comme limite de la suite xn+1 = f(xn), xo quelconque dans E.
Preuve : si xn+1 = f(xn), par hypothèse sur f, on a ||xn+1 - xn || ≤ kn.||x1 - xo||. Montrons que la suite (xn) est une suite de Cauchy dans E. Soit m > n; on peut écrire ||xm - xn || = ||xm - xm-1 + xm-1 - xm-2 + ... + xn+1 - xn ||. Par inégalité triangulaire, on a :
||xm - xn || ≤ (km-1 + km-2 + ... kn) ||x1 - xo || ≤ kn × (1 + k + ... km-n-1) ||x1 - xo ||
Soit finalement :
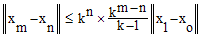
||xm - xn || pourra donc être rendu aussi petit que voulu pour n suffisamment grand car kn et km-n (m > n) tendent vers 0 pour n infini : la suite (xn) est donc une suite de Cauchy dans E qui est complet (espace de Banach), elle converge donc dans E vers une limite L et on aura f(L) = L. L'unicité est évidente car f étant contractante, si L et L' sont deux telles limites, on aura ||f(L) - f(L')|| ≤ k × ||L - L'||, donc : 0 ≤ ||L - L'|| ≤ k × ||L - L'||, ce qui ne se peut sauf si L = L'.
Brouwer et point fixe : » Lipschitz et fonction contractante : »
| Paradoxe de Banach-Tarski : |
 On peut l'énoncer ainsi :
On peut l'énoncer ainsi :
Si l'on admet l'axiome du
choix, il est possible de découper
une sphère en cinq éléments et, à l'aide
d'isométries,
de reconstruire deux sphères de même
rayon que la première.
» Tarski
➔ Pour en savoir plus :