
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|

Historiquement, avec Riemann principalement, la notion d'intégrale est directement au calcul d'aires : aire "sous" la courbe dans le cas d'une fonction numérique positive. L'intégrale d'une fonction est ainsi une mesure de cette fonction. Parler de fonction intégrable, dans le cadre généralisé de Lebesgue, c'est parler de fonction mesurable dans un sens précis que ce dernier développe dans sa nouvelle théorie de l'intégration où la discontinuité n'est plus un obstacle dans la recherche de primitives. Cette "nouvelle" intégrale, qui coïncide sur un intervalle borné avec celle de Riemann pour les fonctions continues, délaisse au second plan l'objectif calculatoire au profit d'un opérateur linéaire sur les fonctions, répondant aux besoins des physiciens du 20è siècle. Elle a également permis la mise en place d'une théorie rigoureuse des probabilités.
➔ La définition qui suit est un cas particulier basé sur un existant sophistiqué qu'est l'intégrale de Riemann. Ce n'est pas celle de Lebesgue. On trouvera in fine (» réf.2a) une construction authentique de la mesure de Lebesgue d'un sous-ensemble de R et une définition rigoureuse de la notion de fonction mesurable (» réf.2b).
| Une mesure sur R fondamentale : la mesure de Lebesgue pour les fonctions numériques continues à support compact : |
X désignant un espace topologique et f : x →R une fonction numérique, on appelle support de f l'adhérence des éléments x de X tels que f(x) ≠ 0, à savoir le plus petit ensemble fermé S tel que f(x) = 0 pour tout x de X \ S (X privé de S).
Une fonction f est dite à support compact pour signifier que son support est une partie compacte de X. Dans notre cas X = R, il s'agit d'une partie fermée bornée.
Une mesure sur R est définie comme une forme linéaire continue sur l'ensemble des fonctions numériques à support compact.
Soit f une fonction numérique continue de support compact [a,b]. F désignant une primitive quelconque de f, on peut associer à f le nombre :
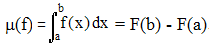
μ(f) correspond donc ici à l'intégrale "usuelle", intégrale de Riemann de f sur l'intervalle [a,b] et, dans ce cas particulier de fonctions, c'est aussi la mesure de Borel-Stieltjes. La linéarité de l'intégrale permet d'affirmer que μ est une forme linéaire. La fonction f étant continue, on peut lui appliquer le théorème de la moyenne sur [a,b] :
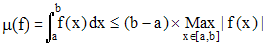
et, en notant M le maximum de f sur [a,b], on a μ(f) ≤ M(b - a) : ce qui assure la continuité de μ.
Mesure de Lebesgue d'un sous-ensemble borné de R :
1A désignant la fonction caractéristique
d'un partie bornée quelconque A de R,
La mesure de Lebesgue de A est, si elle existe, le nombre
μ(1A),
mesure de Lebesgue de 1A
Cette mesure coïncide pour tout intervalle J = [a,b] avec sa "longueur" usuelle : μ(J) = b - a, et si J est réduit à un point, alors μ(J) = 0.
Plus généralement, en
théorie de la mesure, on démontre que tout ensemble fini ou dénombrable est
de mesure nulle : on dit qu'un tel ensemble est
μ-négligeable.
En particulier, N est négligeable et Q, quoique
partout dense dans R, est
négligeable : μ(Q) = 0.
Relativement à la mesure μ,
une propriété P(x) est dite vraie presque partout
(en abrégé : pp) dans R, si
l'ensemble des x de R pour
lesquels elle n'est pas vérifiée est μ-négligeable.
➔ En admettant l'axiome du choix, le mathématicien italien Vitali donna (1905) un exemple d'une partie bornée de R non mesurable au sens de Lebesgue.
|
Intégrale au sens de Lebesgue d'une fonction positive f : |
Soit f une fonction positive; on appelle sommes de Lebesgue les nombres :
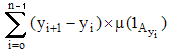
où Ayi désigne l'ensemble des x tels que f(x) < yi avec yo = 0 < y1 < y2 < ... yn. Notons δn la plus grande des différences yi+1 - yi (pas de la subdivision en y). Si, lorsque y1 → 0 et yn→ ∞ de sorte que δn→ 0, les sommes ci-dessus admettent une limite finie indépendante du choix des yi, on dira que la fonction f est intégrable (ou mesurable) au sens de Lebesgue (ou encore m-mesurable).
Cette limite est l'intégrale, au sens de Lebesgue, de la fonction f. On la note encore μ(f) ou, plus concrètement, ∫f dμ. Une fonction f de signe quelconque sera dite intégrable si et seulement si f est mesurable et | f | intégrable.
Lorsque f est à support compact J = [a,b], Riemann subdivise J (à droite) alors que Lebesgue (à gauche) subdivise f(J) :
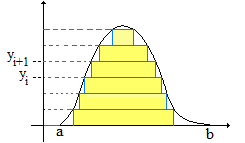
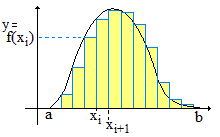
» Lorsque l'on parle de l'intégrale de f, avec la notation ∫f dμ ci-dessus, il s'agit a priori de l'intégrale sur R tout entier. Si l'on s'intéresse à une fonction f restreinte à un intervalle J, on se ramène à une fonction à support compact en posant g(x) = f(x) pour tout x de J et g(x) = 0 sinon, soit g(x) = 1J(x) × f(x).
• Si f est intégrable et si f = g presque partout, alors g est intégrable et ∫f dμ = ∫g dμ.
• Si f est intégrable alors | f | l'est aussi et | ∫f dμ | ≤ ∫| f |dμ.
• Si f est mesurable et si | f | ≤ g avec g intégrable, alors f est intégrable.
|
Une fonction intégrable au sens de Lebesgue mais non au sens de Riemann : |
! Toute fonction intégrable au sens de Riemann l'est aussi au sens de Lebesgue (et les deux intégrales sont alors égales) mais la réciproque est fausse :
Le cas de la fonction de Dirichlet, fonction caractéristique de Q dans R est particulièrement éloquent : comme dit ci-dessus, Q est μ-négligeable, donc μ(1Q) = ∫1Q = 0 : l'intégrale de Lebesgue sur un intervalle [a,b] de la fonction 1Q est donc nulle. Si, dans les sommes de Riemann Sn = Σ(xi+1 - xi)f(ci), on choisit ci rationnel (loisible puisque Q est dense dans R), l'intégrale de Riemann sur [a,b] serait alors Σ(xi+1 - xi) = b - a puisque les ci valent 1. Et si, on choisit les ci réels, les sommes de Riemann sont nulles et l'intégrale de Riemann serait nulle. Ce qui prouve que 1Q n'est pas intégrable au sens de Riemann. Noter qu'intuitivement, on est tenté de penser ∫1Q = 0 : ce qui tend à exprimer l'idée que l'intégrale de Lebesgue, quoique bien plus compliquée dans sa théorie, est plus "naturelle" !
» Lusin
Un théorème de Lebesgue :
Les fonctions numériques intégrables au sens de
Riemann sont les fonctions bornées
à support
compact dont l'ensemble D des points de discontinuité est de mesure nulle
: μ(1D) = 0.
| Espaces Lp (espaces de Lebesgue) : |
Lorsque X désigne un espace topologique muni d'une mesure m, on note Lp(X) l'ensemble des fonctions m-mesurables sur X, à valeur dans R ou C, dont la puissance | f |p est intégrable (p ≥ 1).
Lp(X) est un espace vectoriel et peut être muni de la semi-norme :
![]()
! || ||p n'est pas une norme puisque, comme vu ci-dessus une fonction non nulle peut être d'intégrale nulle. Pour cette raison, on définit dans l'espace Lp la relation f ~ g ⇔ f = g presque partout. C'est une relation d'équivalence et || f ||p= 0 équivaut à f = 0 pp, donc à f μ-négligeable.
L'ensemble des fonctions µ-négligeables est un sous-espace vectoriel N de Lp. Riesz, qui fut à l'origine de l'étude de ces espaces dans le cadre des conditions de convergence des séries de Fourier, prouva que l'ensemble quotient L2/N des classes d'équivalence, espace des (classes de) fonctions mesurables de carré intégrable, est complet (noté simplement L2 lorsqu'il n'y a pas d'ambiguïté).
Théorème de Riesz-Fischer : »
» Parseval , Plancherel , Hölder , Hilbert , Minkowski
➔ Pour en savoir plus :