
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

» Module | Base | Dimension | Th. de la base incomplète | Indépendance linéaire 3D | Sous-espace vectoriel (sev) | Somme de deux sev | Applications linéaires et matrices | Structure d'algèbre | » Espaces affines et applications affines | Produit scalaire et espace euclidien |
![]() Dans cette page,
on pourra rencontrer les abréviations ev et
sev pour signifier respectivement
Dans cette page,
on pourra rencontrer les abréviations ev et
sev pour signifier respectivement
espace vectoriel et sous-espace vectoriel.
Soit (K,+,×) un corps commutatif d'élément unité noté 1. On nomme espace vectoriel sur K, (on dira aussi un K-espace vectoriel) un groupe abélien (E,+) muni d'une seconde loi dite externe, application de K ×E dans E notée ici par un simple point (.), que l'on peut omettre s'il n'y a pas d'ambiguïté, et vérifiant les axiomes suivants :
Si x et y désignent des éléments (on pourra dire vecteurs) de E, a et b désignant des scalaires :
i/ a . (x + y) = a . x + a . y ii/ (a + b) . x = a . x + b . x » produit scalaire , Peano
iii/ a . (b . x) = ab . x 4i/ 1 . x = x
On notera (E,+, .) un tel espace vectoriel.
Les vecteurs du plan ou de l'espace munis de l'addition vectorielle et de la multiplication par un réel constituent des espaces vectoriels.
L'ensemble des fonctions numériques d'une variable x muni de l'addition des fonctions f + g : x → f(x) + g(x) et de la multiplication par un nombre réel définie par αf : x → α × f(x) est un espace vectoriel.
Le corps K est un espace vectoriel sur lui-même. Pour s'en convaincre, il suffit de remarquer que sa multiplication (seconde loi interne ×) peut être aussi considérée comme loi externe !
Par opposition aux vecteurs de l'espace E, les éléments de K, jouant le rôle de nombres (généralement K = R ou C), sont appelés scalaires (du latin scala = escalier, échelle, degré, au sens ici d'échelle de valeurs). La loi externe est souvent appelée multiplication scalaire car elle fait fait intervenir les éléments de K. On parle aussi d'action.
Structure de module :
Lorsque K est un anneau commutatif et unitaire, sans être un corps, on parle de module (le terme est dû à Dedekind) au lieu d'espace vectoriel.
Le terme module désigne également le paramètre p d'une congruence modulo p; on retrouve également ce terme pour désigner la distance | z | à l'origine de l'image M(x,y) d'un nombre complexe z = x + iy, se résumant à la valeur absolue dans le cas réel y = 0.
La notion de vecteurs dans l'histoire des mathématiques : »
Concernant l'axiome iii/ ci-dessus, on parle de condition
d'associativité mixte. On dit que K est un domaine d'opérateurs.
Les conditions iii/ et 4i/ expriment que le groupe multiplicatif K* des
scalaires opère sur E. La condition i/
supplémentaire fait de K un domaine d'opérateurs
distributif. Plus généralement, la notion de groupe
opérant sur un ensemble est très importante en algèbre moderne. Ce
sujet est évoqué au chapitre des groupes.
Dual d'un espace vectoriel, espace vectoriel topologique : »
|
Indépendance linéaire, base, dimension, module libre : |
Une combinaison linéaire d'éléments x, y, z, ... dans un espace vectoriel E sur un corps K, est une écriture de la forme :
a . x + b . y + c . z + ... a, b, c, ... éléments de K.
Si P est une partie de E telle que tout élément de E soit combinaison linéaire d'éléments de P, on dit que P est une famille génératrice (ou un système générateur) de E ou encore que E est engendré par P. Si P est une famille génératrice de E, toute partie G contenant P est aussi génératrice.
Une famille de vecteurs de E dans laquelle toute combinaison linéaire nulle d'éléments a tous ses coefficients nuls est dite libre :
si a . x + b . y + c . z + ... = 0E alors a = b = c = ... = 0k
On dit d'une famille libre que ses vecteurs sont linéairement indépendants. On parle de famille liée pour exprimer qu'elle n'est pas libre. C'est dire qu'au moins un élément de la famille peut s'écrire comme combinaison linéaire des autres (certains coefficients pouvant être nuls mais non pas tous).
On appelle base de E toute partie B de E à la fois génératrice et libre. Un module est dit libre s'il possède une base.
∗∗∗
Dès le collège, la notion de repère
du plan (O,i,j) définit implicitement une base (i,j)
des vecteurs du plan.
On choisit un nouveau repère défini par u = i + j et v =
i - j. Montrer que l'on définit ainsi
une nouvelle base (u,v).
➔ L'intérêt de la notion de base, comparé à celle de partie génératrice, est l'unicité de l'écriture de tout élément de E au moyen de cette base. Un résultat très facile à prouver en supposant l'existence de deux écritures.
Une base d'un espace vectoriel E est une partie génératrice minimale (au sens de l'inclusion). C'est aussi une partie libre maximale.
Dimension :
Si une base possède un nombre fini d'éléments, alors toutes les bases ont le même nombre d'éléments, c'est la dimension de E et on parle d'espace vectoriel de dimension finie.
Si B = (e1, e2, ..., ei, ..., en) est une base, tout élément u de E s'écrit de façon unique comme combinaison linéaire des éléments de B. Les coefficients de cette combinaison sont les coordonnées de u (on dit aussi composantes) dans la base B.
Théorème de la base incomplète :
E étant de dimension finie, toute partie libre non génératrice
peut être complété afin d'obtenir une base.
A contrario, de toute famille
génératrice liée on peut extraire une base.
Preuve : soit n la dimension de E, B = (b1, b2, ..., bn) une base de E et L = (l1, l2, ..., lp), p < n, une famille libre non génératrice. Tant que L reste non génératrice et libre adjoignons lui successivement b1, puis b2, etc. Au bout d'au plus n - p ajouts L deviendra une base de E. En effet, si b1 s'avère combinaison linéaire des li, on choisit alors b2, sinon L = (l1, l2, ..., lp, b1) est libre de cardinal p + 1. Si p +1 < n, on poursuit l'algorithme en notant qu'à chaque étape, il existe au moins un bi non combinaison linéaire des li sinon L engendrerait B et, par là, E lui-même, ce qui ne se peut tant que p < n.
Base canonique d'un espace vectoriel E sur R de dimension finie n :
à titre d'introduction, considérons le cas de R2 = R × R, espace vectoriel de dimension 2 sur R, muni de la loi externe (multiplication sclaire), α.(x,y) = (αx,αy) pour tout réel α et tout couple (x,y) de R2. Un tel couple s'écrit :
(x,y) = x.(1,0) + y.(0,1)
et c'est la façon la plus élémentaire et la plus commode d'exprimer un couple de R2. Posons i = (1,0) et j = (0,1). Le couple (i,j) est une base de R2 : on parle de base canonique de R2 (au sens latin du terme canonicus = conforme aux règles, prenant ici le sens de la plus naturelle).
Plus généralement, dans toute base d'un espace vectoriel réel E de dimension n, les coordonnées (x1, x2, ...,xn) d'un vecteur constituent un n-uplet de nombres réels. En posant e1 = (1, 0, 0, ...0), e2 = (0, 1, 0, ...0), ... , en = (0, 0, 0, ...1), on définit la base canonique de l'espace E qui s'identifie ainsi à Rn.
L'ensemble M2(R) des matrices carrées d'ordre 2 à termes réels est un espace vectoriel sur R de dimension 4 :
![]()
» On peut encore parler ici de la base canonique de M2(R).
L'ensemble
Φ des fonctions numériques
définies sur R, munis de l'addition des fonctions et
de la multiplication par un réel, est un espace vectoriel
de dimension infinie.
Il suffit de remarquer
que Φ
contient le sous-espace
des polynômes de degré quelconque dont une base est
(eo, e1, e2, ..., en,
...) où en désigne le monôme
défini par en(x) = xn , n∈N.
Le corps R des nombres réels est un espace vectoriel de dimension 1 sur lui-même, mais de dimension infinie sur le corps Q des rationnels. La première partie de cette assertion est triviale. La seconde l'est moins : considérer l'ensemble P des nombres réels s'écrivant sous la forme :
qo
+ q1π
+ q2π2
+ ... + qnπn
, n∈N
, les qi étant des nombres
rationnels.
P est un espace vectoriel sur R
(sous-espace vectoriel
de R). Si P est de dimension finie, alors la famille des puissances de
π
étant génératrice, on
peut en extraire une sous-famille finie qui sera une base de P. On pourrait
alors exprimer, dans cette base, une puissance de
π non élément de cette base :
c'est dire qu'il existerait un polynôme à coefficients rationnels dont
π serait solution. Mais
on sait que
π
n'est pas un nombre algébrique.
Par suite P
est de dimension infinie et également R, qui contient P, a fortiori.
∗∗∗
Montrer que C2 =
C × C est un espace vectoriel de dimension 2 sur C mais de
dimension 4 sur R.
De façon analogue C3 est un espace vectoriel de dimension 3 sur
C mais de
dimension 6 sur R.
| Droite vectorielle, plan vectoriel : |
Un espace vectoriel de dimension 1 (resp. 2) est une droite vectorielle (resp. plan vectoriel). Notre espace usuel (3 dimensions) peut être considéré comme un ensemble de points (espace affine); un couple de points (A,B) définit un vecteur AB. On peut alors parler de vecteur u pour exprimer la classe d'équipollence de (A,B).
Un plan affine de l'espace est défini par un de ses points et un couple de vecteurs libres définissant sa direction (plan vectoriel).
Une droite d'un plan ou de l'espace (droite affine) est définie par un de ses points et un vecteur (sa direction aussi appelé vecteur directeur).
Exemple de plan vectoriel : Dans un espace vectoriel de dimension 3 de base (i,j,k), l'ensemble (p) des vecteurs V tels que V(x, y, z) tels que x + y - z = 0 est un plan vectoriel de base (u,v) =(i + k, j + k) ; en effet, pour tout vecteur V de (p), V(x, y, z) = V(x,y,x + y); donc V ∈ (p) ⇔ V = x.u + y.v avec u = i + k et v = j + k et ces vecteurs sont linéairement indépendants car x.u + y.v = 0 ⇔ x = y = 0.
➔ Deux vecteurs du plan V(a,b) et W(c,d) sont linéairement indépendants et forment donc une base si et seulement si leur déterminant ad - bc est différent de 0.
Dans l'espace, deux vecteurs V(a,b,c) et W(a',b',c') sont linéairement indépendants et forment alors une base d'un plan vectoriel (sous-espace vectoriel de dimension 2) si et seulement l'un des 3 déterminants d'ordre 2 formés sur le ableau de coordonnées est non nul :

C'est dire que V et W sont liés si les trois déterminants ci-dessus sont nuls :
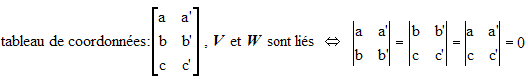
Vecteurs du plan : » Produit scalaire : » Gibbs et le produit vectoriel : »
|
Sous-espace vectoriel : |
Soit F est une partie d'un K-espace vectoriel (E,+, .). Si, muni des lois d'espace vectoriel de E (lois induites), une partie F est lui-même un espace vectoriel, on dit que F est un sous-espace vectoriel de E.
! Il n'est en effet pas pas certain que le résultat des opérations E appliquées à des éléments de F, soit un élément de F :
Dans l'espace vectoriel E des vecteurs du plan, considérer l'ensemble F des vecteurs dont le produit xy des coordonnées est positif : u(2;7) et v(-3;-5) sont éléments de F mais pas leur somme w(-1;2). On dit que F n'est pas stable pour l'addition : F n'est pas un sev de E.
Théorème :
Une partie non vide F d'un K-espace vectoriel E est un sous-espace vectoriel de E si et seulement si pour tout couple (x,y) de F × F et tout couple (a,b) de K × K, a.x + by est élément de F : toute combinaison linéaire d'éléments de F est un élément de F.
On peut, si l'on préfère, vérifier séparément, ce qui est équivalent, que
a/ F est non vide;
b/ Pour tous x et y de F, leur somme x + y est un vecteur de F;
c/ Pour tout réel a, a.x est un vecteur de F.
Toute intersection (finie ou non) de sev est un un sev.
! Il n'en est pas de même de la réunion :
Considérer dans R2, espace vectoriel sur R, F = {(a,0), a réel} et G = {(0,b), b réel}. F et G sont des s.e.v. de R2 mais leur réunion n'en est pas un : considérer u = (1,0) ∈F et v = (0,1)∈G, u et v sont éléments de F ∪ G mais pas u + v = (1,1) car dans F ∪ G l'une au moins des coordonnées est nulle. Mais F∩G = {0,0)} est un s.e.v. de R2 !
Un résultat bien évident... :
Si E est de dimension finie, alors dim F ≤ dim E
Un sous-espace vectoriel de dimension 1 (resp. 2) est une droite vectorielle (resp. plan vectoriel). Plus généralement, en dimension n, on appelle hyperplan vectoriel un sous-espace vectoriel de dimension n - 1.
∗∗∗
1. Prouver que l'ensemble E des fonctions affines de
R
sur R, fonctions de la forme fa,b : x
→ ax
+ b, est un ev de dimension 2 dont la
paire
{u : x
→ x
, v : x → 1}
est une base.
2.Vérifier que l'ensemble des matrices diagonales de la
forme
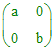 constitue un sous-espace vectoriel
de dimension
2 dans l'espace vectoriel
M2(R).
constitue un sous-espace vectoriel
de dimension
2 dans l'espace vectoriel
M2(R).
Applications linéaires & matrices : »
|
Somme de sous-espaces vectoriels, somme directe : |
On appelle
somme
de deux sous-espaces F et G de E, l'ensemble S des éléments x + y, où x est
élément de E et y élément de F. Il est facile de vérifier que muni des
opérations d'espace vectoriel de E, S en est un sous-espace vectoriel.
La somme S est directe lorsque S = E et que F et G n'ont que le vecteur nul de E en commun, c'est à dire F∩G ={0E}; on écrit alors : E = F ⊕ G et on dit aussi que F et G sont supplémentaires dans E. Tout vecteur de E s'écrit alors de façon unique comme somme d'un élément de f et d'un élément de G.
» En effet, si deux écritures x + y et x' + y' étaient possibles, on pourrait écrire : x - x' = y' - y; mais le membre de gauche est dans F et celui de droite dans G et comme F∩G ={0E}, il suit que x - x' = y' - y = 0E. c'est dire que x = x' et y = y'.
! Il n'est pas dit que F∩G est l'ensemble vide. Ce n'est pas possible dans le cas de deux sev de E : ils ont au moins 0E en commun. Remarquer également qu'un sev ne possède généralement pas un unique supplémentaire. Dans l'ev des vecteurs du plan, un supplémentaire de toute droite vectorielle engendré par u (sous-espace de dimension 1) est une droite vectorielle quelconque engendrée par un vecteur non colinéaire à u.
∗∗∗
L'intersection de deux sous-espaces vectoriels est un sous-espace vectoriel.
C'est bien évident...
Justifier, par contre, que la réunion de deux sous-espaces vectoriels n'en est
pas un, à moins que l'un soit inclus
dans l'autre ! (étudier la somme de deux éléments pris dans chaque sev)
Théorème des dimensions :
Si E est dimension finie et somme directe de F et G, alors dimE = dim F + dim G.
» Grassmann Applications linéaires : noyau & image : ».
|
Espace vectoriel quotient : |
Lorsque F est un sous espace vectoriel de (E, +, .), la relation définie dans E par x ~ y ⇔ x - y ∈F est une relation d'équivalence (vérifiez-le !). L'ensemble quotient, noté E/F, ensemble des classes d'équivalence muni des opérations induites, est un espace vectoriel :
Structure quotient : »