ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 LIPSCHITZ
Rudolf, allemand, 1832-1903 |
Après des études à la
célèbre université de Königsberg
et à Berlin où il obtint son doctorat (1853) sous la direction de Dirichlet
et Ohm. Sa thèse, écrite en latin, fut traduite par Montel), Rudolf Otto Sigismund Lipschitz enseigna
au lycée de Königsberg.
En 1857, Lipschitz obtient un poste à l'université de Berlin (1857) puis à Breslau (autrefois prussienne, actuelle ville de Wroclaw en Pologne depuis 1945) et enfin à Bonn (1864) où il fut, avec Plücker, le directeur de thèse de Felix Klein en 1868.
Ses travaux concernent la théorie algébrique des nombres (systèmes hypercomplexes, algèbre de Lipschitz), les variétés riemanniennes, les équations différentielles aux dérivées partielles et les systèmes différentiels où il confirma et précisa des résultats de Cauchy :
| Condition de Lipschitz, fonction lipschitzienne, fonction contractante : |
Dans un espace métrique ou vectoriel normé E, une fonction f vérifie la condition de Lipschitz, dite aussi de
Hölder, d'ordre a > 0, de rapport k > 0, si pour tout (x,y) :Lorsque a = 1, la fonction est dite lipschitzienne. Si, de plus, k < 1, la fonction est dite contractante. Une fonction lipschitzienne est uniformément continue sur E.
➔ Lorsque E = R muni de sa distance usuelle d(x,y) = | x - y | (valeur absolue) dire que la fonction f est lipschitzienne de rapport k > 0 signifiera que pour tout couple (x,y), on a | f(x) - f(y) | ≤ k.| x - y |.
Les fonctions affines x → ax + b sont lipschitziennes sur R.
La fonction x → 1/x est lipschitzienne contractante sur ]1,+∞[ mais non lipschitzienne sur ]0,1[.
Si f et g sont lipschitziennes, il en est de même de f + g et λf pour tout réel λ. Les fonctions constituent donc un sous-espace vectoriel de F(R), espace vectoriel des fonctions numériques définies sur R. Résultat identique si on limite l'ensemble de définition de f à un intervalle I de R.
Théorèmes :
Toute fonction dérivable sur un intervalle J de R, de dérivée bornée par k sur J est lipschitzienne de rapport k
Inversement :
Toute fonction dérivable et lipschitzienne
de rapport k sur un intervalle J de R vérifie | f
'(x)|
≤ k sur J.
Un point fixe d'une fonction f : E → E est un point de E invariant par f, c'est à dire tel que f(x) = x.
Lorsque f est un espace de Banach, toute fonction contractante de E dans lui-même admet un unique point fixe.
Problème de Cauchy : » Théorème du point fixe de Brouwer : »
∗∗∗
1. a) Prouver
que x → | x | et est lipschitzienne.
b) Prouver que la composée de deux fonctions lipschitziennes
est également lipschitzienne.
c) En cherchant à faire apparaître f(x) - f(y) et g(x) - g(y)
dans la différence (f × g)(x) - (f × g)(y),
trouver une condition sur f et g afin que la
fonction produit de deux fonctions lipschitziennes soit
lipschitzienne.
2. On suppose que f∈F(R)
est contractante et on pose g(x) = f(x) - x.
a) Prouver que la fonction g est lipschitzienne.
b) Prouver que g est strictement décroissante et réalise une
bijection continue de R sur R.
Afin
de calculer les limites de g en ±∞,
rechercher un encadrement de g(x) en remarquant que |
f(x) - f(o) |
≤ (1 - u).|
x | avec 0 < u < 1.
| Théorème de Lipschitz pour les systèmes différentiels : |
Ce théorème généralise aux systèmes différentiels du 1er ordre la solution du problème de Cauchy : quitte à augmenter le nombre d'inconnues yk fonctions de x, et donc le nombre d'équations du système, on peut se ramener au cas où seules les dérivées premières interviennent dans le système.
Soit donc un système différentiel écrit sous la forme (dite explicite -ou résolue- par rapport aux dérivées premières) :
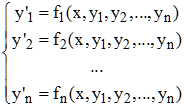
En notant respectivement Y et Y' les matrices colonnes d'éléments y1, ... yn et y'1, ... y'n, le système s'écrit :
Y' = f(x,Y)
Soit (xo,Yo) donné. S'il existe un voisinage V de (xo,Yo) dans lequel (x,Y) → f(x,Y) est continue et lipschitzienne relativement à Y, alors il existe une unique solution du système contenant (xo,Yo).
Résolution d'un système différentiel linéaire : 2×2 | 3×3
|
Quaternions de Lipschitz : |
Lorsque les composantes a, b, c et d d'un quaternion d'Hamilton a + bi + cj + dk sont choisies dans l'anneau Z des entiers relatifs, on parle de quaternions de Lipschitz. Dans ce cas, muni des opérations induites par le corps H des quaternions, ce sous-ensemble n'est plus un corps mais un anneau.
Plus généralement :
On appelle quaternion d'Hurwitz un quaternion dont les quatre composantes sont soit dans Z soit dans ½ + Z, pour signifier les nombres de la forme ½ + n, n∈Z. Ils constituent un anneau euclidien (donc factoriel).
» Hurwitz
➔ Pour en savoir plus :
Neumann
Karl Gootfried