ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 RADEMACHER Hans Adolph,
américain, 1892-1969 |
D'origine allemande, Rademacher fit des études supérieures de
mathématiques à Göttingen où il obtint son doctorat (1916) sous la direction de
Caratheodory portant sur la
théorie de la mesure. Après plusieurs postes d'enseignement en Allemagne, il
doit s'exiler aux Etats-Unis afin d'échapper au pouvoir nazi (1933).
Éminent professeur à l'université de Pennsylvanie, ses travaux portent tout particulièrement sur la théorie analytique des nombres (nombres premiers, théorie additive des nombres où il apporte (1943) une solution au fameux problème de la partition d'un entier naturel au moyen de l'analyse complexe, un casse-tête initié par Goldbach et dont Ramanajan avait donné une solution approchée en 1918.
Rademacher tenta de prouver l'hypothèse de Riemann, sur les zéros de la fonction ζ (zêta) émise en 1859, laquelle est encore (décembre 2016), un problème ouvert : rappelons ici cette célèbre conjecture portant sur les fonctions définies par :
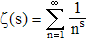
Lorsque s est complexe, s = σ + it (σ et t sont respectivement les parties réelle et imaginaire de s), ces séries sont absolument convergentes lorsque σ > 1. Elles divergent sinon mais peuvent être prolongées analytiquement pour tout s ≠ 1. Et Riemann énonça l'hypothèse suivante :
Lorsque la partie réelle de s est comprise entre 0 et 1, les zéros de ζ(s) ont tous 1/2 pour partie réelle (σ = 1/2)
Hypothèse de Riemann, hypothèse généralisée : »
➔ Pour en savoir plus :
,
par Hans Rademacher, Ed. Blaisdell, 1964.
Julia