ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

L'arithmétique d'Euclide     » Division euclidienne, multiples et diviseurs
       » PGCD et nombres premiers entre eux | PPMC | Nombres premiers
       Exercices tout au long de cette page, voir aussi :  CM2/CLG , LYC , SUP

Dans le livre VII de ses Éléments, Euclide définit tout d'abord le concept naturel de nombre, sous-entendu entier. Voici en particulier quelques unes de ses définitions :

• L'unité est ce selon quoi chacune des choses existantes est dite une;

• Un nombre est un assemblage composé d'unités.

• Un nombre est multiple d'un nombre, le plus grand du plus petit, quand il est mesuré
  par le plus petit.

 » cette définition du concept de multiple d'un nombre exprime que l'addition répétée du plus petit finira par fournir le plus grand : si a > b, alors b + b +... + b = a. Autrement dit, il existe un entier n tel que n × b = a.

• Le nombre pair (resp. impair) est celui qui peut (resp. ne peut pas) se partager en deux parties égales (sous-entendu entières).

• Est dit premier le nombre qui est mesuré par l'unité seule (il n'est multiple que de 1).

• Est dit composé le nombre qui est mesuré par quelque (n'importe quel) nombre (autre que l'unité).

Euclide étudie ensuite la divisibilité, les nombres premiers, puis la proportionnalité pour en arriver (Livre X) aux grandeurs commensurables, rationnelles et irrationnelles, reprenant ainsi les travaux de Pythagore est ses disciples.

La notion de grandeur et de commensurabilité : »

∗∗∗ Proposition XI, livre VII
Si le tout est au tout comme le nombre retranché est au nombre retranché, le nombre restant sera aussi au nombre restant comme le tout est au tout.
Traduire en langage moderne sachant que a est à b ce que c est à d signifie a/b = c/d   ☼

La division euclidienne, multiples et diviseurs :

Pour tout couple (a,b) d'entiers naturels, b étant non nul, on peut écrire :

a = b × q + r, q et r entiers et 0 ≤ r < b

On dit que q est le quotient de la division euclidienne de a par b, appellation due au groupe Bourbaki (Théorie des ensembles, Ch. 3, §5, n°6) dans son entreprise de rénovation des mathématiques. L'entier r est le reste. L'entier a est le dividende (celui que l'on divise), b est le diviseur.

La condition 0 ≤ r < b assure l'unicité du quotient et du reste. Lorsque r est nul, a = b × q, on dit que a est un multiple de b ou que b est un diviseur de a ou encore que a est divisible par b.

Compléments sur multiples et de diviseurs : »

 ➔   Un cas très particulier : si a est nul, q = r = 0. 0 est multiple de tout entier.

Dans un passé récent, on appelait partie aliquote d'un nombre n (du latin aliquot = un certain nombre de), un diviseur de n autre que n lui-même. Le sens étymologique est clair : si d divise n, d distinct de n, alors d est contenu un nombre entier de fois dans n.

∗∗∗
2. On emballe 640 CD dans des boîtes pouvant en contenir 27. Seule la dernière boîte n'est pas pleine. Combien de CD contient-elle ?
Rép. : 640 = 27 × 23 + 19 : dans 640, il y a 23 fois 27 et il reste 19. On utilise donc 24 boites et la dernière ne contient que 19 CD.

 !  Collégiens & lycéens : Certaines calculatrices actuelles, utilisées au collège et au lycée, pratiquent la division euclidienne au moyen d'une touche spéciale. Celles qui ne possèdent pas cette fonction possèdent toutes aujourd'hui la touche "a b/c" mettant une fraction n/d sous la forme a + b/c. Le piège, chez certains constructeurs, est que la fraction b/c est affichée simplifiée et irréductible.

Par exemple : quel est le reste de la division euclidienne de 348 par 24 ? la machine répond par une écriture symbolique, quelque chose comme : 14 ¬ 1 ¬ 2 laissant à penser que le quotient est 14 et le reste 1... En fait 348 = 14 × 24 + 12. La calculatrice a trouvé a + b/c = 14 + 1/2, soit 14 + 12/24 : il faut penser à réécrire b/c avec le diviseur comme dénominateur !

Discussion :    

On peut, plus généralement, permettre à a et b d'être négatifs  (b non nul). On se place dans le cas a non nul, non multiple de b :

i/  a∈N*, b∈N* (division euclidienne arithmétique) :

Considérons la suite d'entiers b, 2b, 3b, ..., nb, ... et posons S = {b, 2b, 3b, ..., n × b, ...}. S n'est pas borné supérieurement. Lorsque a > 0, division dans N : le diviseur b étant strictement positif, il existe n∈N tel que a < n × b. Soit p la plus petite valeur de n pour qu'il en soit ainsi. Cet entier p est au moins égal à 1. Posons q = p - 1. Par définition de p, on a alors a  > qb et a < pb < (q + 1)b. Donc bq < a < b(q + 1), r = a - bq vérifie 0 < r < b (et r serait nul pour a multiple de n).

Dans la division euclidienne de a par b, de quotient q, de reste r, on a a = bq + r
avec bq ≤ a < b(q + 1), r = a - bq, 0 ≤ r < b  (r = 0 ⇔ a = bq ⇔ a multiple de b)

 ➔   Dans l'ensemble des nombres rationnels, on peut écrire q ≤ a/b < q + 1 : q apparaît comme la partie entière de la fraction a/b. La conjonction de r = a - bq et 0 ≤ r < b implique bq ≤ a < b(q + 1). On peut se limiter à exprimer :

Dans la division euclidienne de a par b, de quotient q, de reste r, on a :
a = bq + r avec r = a - bq, 0 ≤ r < b  (r = 0 ⇔ a = bq ⇔ a multiple de b)

ii/  a∈Z*, a < 0, b∈N* :

Lorsque a < 0, on effectue la division euclidienne (cas précédent) de | a | par b :  | a | = bq + r, 0 < r < b. Vu que a = -| a |, on obtient en remplaçant : a = -bq - r = -bq - b + b - r. Posons q' = -q - 1,  r' = b - r. On a : a = bq' + r' avec 0 < r = b - r' < b, donc -b < -r' < 0, soit 0 < r' < b.

iii/  a∈Z, b∈Z*, b < 0 :

 On se ramène à i/ en écrivant l'égalité de la division euclidienne de | a | par | b |, à savoir | a | =  | b |q + r avec 0 < r < | b |. Si a > 0, a = b(-q) + r. Le quotient est q' = -q, le reste est r. Si a < 0, -a = b(-q) + r, soit a = bq - r = b(q + 1) + (-b - r) = bq' + r' avec  q' = q + 1 et r' = - r - b. On a 0 < r < -b, donc 0 < -r' - b < -b, soit : b < r' < 0 ou encore 0 < r' < -b = | b |.

On peut énoncer en conclusion :

 a et b désignant un couple d'entiers de Z × Z*, il existe un unique couple (q,r) de Z × N tel que
a = bq + r, avec 0 ≤ r < | b |, le cas r = 0  correspondant à a multiple de b.

 ➔   On montrera facilement en corollaire que :

Dans la division euclidienne de a par b, si l'on multiplie a et b par un même entier k ≠ 0,
le quotient est inchangé et le reste est multiplié par k.

Multiples & diviseurs, divisibilité : »         Divisibilité dans un anneau : »

Notion de congruence : »         Anneau quotient Z/nZ des classes résiduelles modulo n : »

∗∗∗ division euclidienne          » PGCD/PPCM

1.  Vérifier l'égalité 1111 = 24 × 45 + 31. De quelle division euclidienne, cette égalité résulte-t-elle ?
Rép. : 1111 divisé par 45 car le reste doit être inférieur au diviseur.

2.  Vérifier l'égalité 3970 = 62 × 63 + 64. Cette égalité résulte-t-elle d'une division euclidienne ?
Quel est le quotient de la division euclidienne de 3970 par 62 ? Quel est le reste de la division euclidienne de 3970 par 63 ?
Rép. : Cette égalité est juste mais c'est un piège car 64 > 62 et 64 > 63. On extrait 62 de 64 que l'on "déplace" dans le produit : 3970 = 62 × 64 + 2
le quotient est 64 (reste 2). Quant au reste de la division de 3970 par 63, on peut écrire 3970 = 63 × 63 + 1.Le reste est donc 1.

3. (niveau 3ème)  On considère deux entiers; dans la division du plus grand par le plus petit puis par le double du plus petit, on a trouvé 17 comme quotient et 11 pour reste dans le premier cas, 8 et 23 dans le second cas. Quels sont ces deux nombres ?
Rép. : Si on appelle x et y ces nombres, x étant le pus grand, on a : x = 17y + 11 et y = 8 × 2x + 23. On trouvera x = 215 et y = 12.

2.  Montrer que tout entier naturel est le produit d'un nombre impair par une puissance de 2, c'est à dire de la forme 2p(2n + 1), p et n entiers.

5. (niveau 6ème/5ème) Des petits problèmes faisant intervenir la division euclidienne.   
 
Les nombres premiers :

On doit à Euclide l'étude et la première preuve de l'infinitude de l'ensemble des nombres premiers : nombre n'ayant aucun diviseur propre (diviseur non trivial : autre que 1 et lui-même), et de l'existence, pour tout entier naturel n au moins égal à 2, d'un diviseur premier p dont le carré est inférieur à n, ce qui permet la recherche de primarité (ou primalité en franglais).

Un nombre non premier est dit composé : il admet au moins un diviseur autre que 1 et lui-même (donc plus de deux diviseurs).

Distribution des nombres premiers : »           Infinitude des nombres premiers : »          » Ératosthène      

 i  le chiffre 1 fut considéré comme premier jusqu'au tout début des années 1960, à l'aube de l'avènement et de l'enseignement des mathématiques dites modernes. La définition était alors : est premier tout nombre (entier) qui n'est divisible que par lui-même et par l'unité (cours d'algèbre, Lebossé et Hemery, classe de quatrième, 1947) :

 

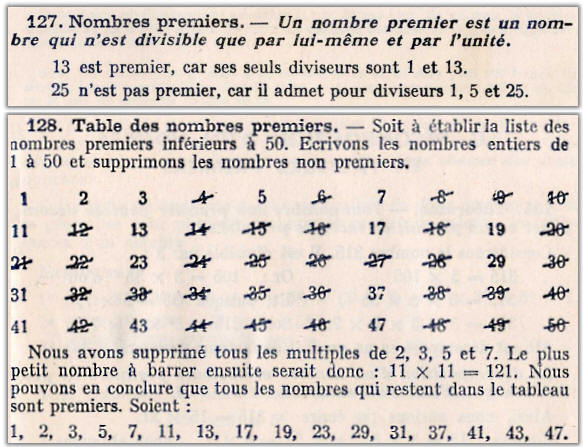
Lorsqu'on travaille sur des problèmes d'arithmétique, nombres premiers en particulier, on étudie constamment des propriétés de divisibilité et il s'avère souhaitable que l, diviseur universel, certes respectable, ne soit pas premier. D'où la définition actuelle éliminant l'unité, laquelle ne possède qu'un seul diviseur : lui-même.

Théorème :    

Tout entier naturel n admet une unique factorisation de la forme n = p1α × p2β × ... × pkγ
où les p1, p2,..., pk sont les diviseurs premiers de n et α, β, γ, ... des entiers non nuls.

Preuve et application JavaScript : »

Corollaire :  

Si n est un entier composé (non premier), alors n admet un diviseur premier p tel que p2 ≤ n

Ce théorème fondamental d'arithmétique fit l'objet des propositions XXXIII et XXXIV des Éléments d'Euclide. Il est parfois appelé théorème d'Al-Farisi en l'honneur du mathématicien perse (1260-1320) à qui l'on doit sa première démonstration en termes "modernes".

Nombre de diviseurs :     

Soit  n = p1α × p2β × ... × pkγ  la décomposition en facteurs premiers d'un entier n non premier.
Son nombre de diviseurs ( y compris 1 et lui même) est le produit : (α+1) × (β+1) × ... × (γ+1)  avec α, β,  ... γ non nuls.

       Preuve : »       Recherche de nombres premiers : »         Divisibilité dans un anneau : »

Plus grand diviseur commun (PGDC ou PGCD) à deux nombres entiers, nombres premiers entre eux  :

  • Le plus grand diviseur commun à 24 et 18 est 6. En effet 24 = 2 × 2 × 2 × 3 et 18 = 2 × 3 × 3. Le pgcd est donc 2 x 3 = 6.

Vocabulaire :    

 ➔  On parle le plus souvent de PGCD (Plus Grand Commun Diviseur) au lieu de PGDC (Plus Grand Diviseur Commun). Il s'agit là de l'influence allemande et anglo-saxonne : dans la langue de Gauss, on parle de Größter Gemeinsamer Teiler (ggT),  soit,  en anglais Greatest Common Divisor (GCD). Idem pour le Plus Petit Multiple Commun (PPMC ou PPCM). : en allemand kleineres gemeinsames Vielfaches (kgV), en anglais : Least Common Multiple (LCM).

Cette notion s'étend à plusieurs nombres :

Par exemple : Quel est le plus grand diviseur commun à 126, 140 et 350 ?  126 = 2 x 3 x 3 x 7 , 140 = 2 x 2 x 5× 7 et 350 = 2 x 5 x 5 x 7.
                        Rép. = 2 x 7 = 14.

On voit, au-delà du collège (où la notion de pgcd est au programme), que l'on peut retenir :

Le pgdc de plusieurs nombres est égal au produit de tous les facteurs premiers communs
à ces nombres affectés de leur plus petit exposant

Deux nombres dont le PGCD est égal à 1, sont dits premiers entre eux ou encore : étrangers.

  • Par exemple 12 et 35 sont premiers entre eux et cependant aucun de ces nombres n'est premier puisque 12 = 3 × 4 et 35 = 5 × 7. On écrit donc pgcd(12,35) = 1. On dit aussi que 12 est premier avec 35.

Cette notion de nombres premiers entre eux s'étend à plusieurs nombres pour signifier que, pris deux à deux, le pgcd est égal à 1.

  • Par exemple 12, 25 et 91 sont premiers entre eux puisque pgcd(12,25) = 1, pgcd(12,91) = 1 et pgcd(25,91) = 1. On peut écrire : pgcd(12,25,91) = 1.

 ➔  Si à tout couple d'entiers, on associe son pgcd, on définit ainsi une opération dans N. Posons pgcd(a,b) = a ^ b. Cette loi de composition interne est associative :

(a ^ b) ^ c = a ^ (b ^ c)

On parle aussi de nombres premiers entre eux dans leur ensemble si a ^ b ^ c = 1 en écrivant :

a ^ b ^ c = (a ^ b) ^ c = a ^ (b ^ c)

Ainsi, 6, 9 et 10 sont premiers entre eux dans leur ensemble car 6 ^ 9 ^ 10 = (6 ^ 9) ^ 10 = 3 ^ 10 = 1 et cependant, ils ne sont pas premiers deux à deux car 6 ^ 9 = 3 et 6 ^ 10 = 2.

La définition récursive du pgcd (procédure qui fait appel à elle-même) peut s'écrire :

pgcd(a,b) = pgcd(b,r), avec la condition d'arrêt pgcd(a,0) = a

où r désigne le reste de la division de a par b (» division euclidienne). C'est la définition choisie par Euclide pour établir son algorithme de recherche. Cette notion de récursion, fondamentale dans les algorithmes mathématiques et informatiques, permet des programmes de calcul très concis. Au collège, elle permet une recherche aisée du pgcd de deux entiers :

PGCD selon Euclide (étude de l'algorithme et programmation JavaScript) : »

∗∗∗
On peut aussi se débrouiller sans algorithme... Calculer le pgcd de 1053 et 975, puis simplifier la fraction 975/1053..
Rép. : 1 + 5 + 3 = 9 : 1053 est divisible par 9. 1053 = 9 × 117. 1 + 1 + 7 = 9. tiens donc ! Finalement 1053 = 92 × 13.
Quant à 975, 9 + 7 + 5 = 21. Ce nombre est donc divisible par 3 et aussi par 25 (puisqu'il se termine par 75).
Ainsi 975 = 52 × 3 × 13 et le pgcd est 39. D'où 975/1053 = 25/27 (en simplifiant par 3 × 13 = 39).

On peut également procéder par différences :

PGCD par différences (étude de l'algorithme et programmation JavaScript) : »
 
PPMC de deux entiers (plus petit multiple commun) et cas de plusieurs nombres :      

Dans les calculs fractionnaires et certains problèmes arithmétiques, il est aussi utile de connaître le plus petit multiple commun de deux entiers : c'est le PPMC ou PPCM ( remarque).

  • Considérons 24 = 2 x 2 x 2 x 3 et 90 = 2 x 3 x 3 x 5. On ne choisit pas le facteur 3 de 24, car il est au carré dans 90 et on ne choisit pas le 2 de 90 car on l'a déjà au cube dans 24. Le ppmc sera donc 2 x 2 x 2 x 3 x 3 x 5  = 8 x 9 x 5 = 360.

Cette notion s'étend à plusieurs nombres et le PPMC devient vite assez grand... mais, en général plus petit que le produit des nombres entrant en jeu :

  • Quel est le PPCM de 126 , 140 et 550 ?  126 = 2 x 3 x 3 x 7 , 140 = 2 × 2 × 5 × 7 et 550 = 2 × 5 × 5 × 11.
    Rép. =     2 × 2 × 3 × 3 × 5 × 5 × 7 × 11 = 69 300. Le produit est 9 702 000

On pourra retenir que :

Le PPCM de plusieurs nombres est égal au produit de tous les facteurs premiers communs ou non
à ces nombres affectés de leur plus grand exposant

 ➔   On remarque dans l'exemple de 24 et 90 qu'on a laissé de côté les diviseurs communs avec leur plus petit exposant : le produit de ces diviseurs est donc le PGCD de 24 et 90. Ce qui montre que d'une façon générale  :

∗∗∗

4.   Introduction au PGCD par un exercice élémentaire

5.  On doit remplir de cubes une caisse dont les dimensions, en cm, sont 150, 165 et 105. Quelle sera la plus grande des mesures possibles de l'arête des cubes ? 

Rép : pgcd(150,165, 105) = 15 car 150 = 2 x 3 x 5 x 5 , 165 = 3 x 5 x 11 et 105 = 3 x 5 x 21.

6.  Quel est le plus petit multiple commun aux dix premiers nombres entiers (non nuls) ?

Rép : 2520.

7.  Quel est le plus grand nombre de 3 chiffres qui, divisé par 3, 7 et 11 donne toujours le même reste 2 ? 

Rép : si n est ce nombre, n - 2 est multiple de 3, 7 et 11. 3, 7 et 11 sont premiers entre eux. Donc n - 2 est multiple de 231. On a déduira n = 926.

8.  Quel est le plus grand nombre de 3 chiffres qui, divisé par 6, 9 et 12 donne toujours le même reste 5 ? 

Rép : si n est ce nombre, n - 5 est multiple de 6, 9 et 12. Mais ces nombres ne sont pas premiers entre eux. Leur ppmc est 36. Donc n - 5 est multiple de 36. Plus grande valeur de n possible : pour éviter de tâtonner, on divise 999 - 5 par 36 : le quotient entier est 27.
On en déduit n = 27 x 36 + 5 = 977.

9.  Dans une gare de la région parisienne, les quais A, B et C desservent 3 destinations. dès 5h30 du matin, il y a un départ sur A, B et C respectivement toutes les 15, 25 et 18 minutes. A quelle heure y aura-t-il, pour la première fois, un départ simultané de trois trains ?

Rép : Soit T le nombre de m x 5, 18 = 2 x 3 x 3 et 25 = 5 x 5. Par conséquent T = 3 x 5 x 2 x 3 x 5 = 450. 450 minutes sont 7h 30 min. Le 1er départ simultané au lieu à 13 h.

10.    a)  Montrer que si deux entiers naturels x et y sont premiers entre eux, il en est de même de 2x + y et 5x + 2y.
         b)  En déduire les solutions du système ab = 3m, (2a + b)(5a + 2b) = 1620, m désignant le ppmc de a et b.

Rép : a) 2(2x + y) + x = 5x + 2y. Donc si d divise 2x + y et 5x + 2y, alors d divise x. Or, 3(2x + y) - x - y = 5x + 2y. Donc si d divise 2x + y et 5x + 2y, comme il divise x, il devra diviser y. Inversement si d divise x et y, il divise évidemment 2x + y et 5x + 2y. Les paires {x,y} et {2x + y,5x + 2y} ayant les mêmes diviseurs, elles ont le même pgcd. Par conséquent si pgcd(x,y) = 1, alors pgcd(2x + y,5x + 2y) = 1.

b) ab = pgcd(a,b) × ppmc(a,b), donc pgcd(a,b) = 3. Posons a = 3a' et b = 3b'. On a (2a' + b')(5a' + 2b') = 1620/9 = 180 avec a' et b' d'une part et  2a' + b' et 5a' + 2b' d'autre part sont premiers entre eux Or, 180 = 22 x 32 x 5 et le plus petit facteur est 2a' + b'. Les facteurs devant être premiers entre eux, ce dernier est donc nécessairement choisi dans {22, 5, 32}. On remarque que 5a' + 2b' - 2(2a' + b') = a'. On procède par essais et élimination des cas :

  • 2a' + b' = 4 , 5a' + 2b' = 45 : a' = 37 incompatible avec 2a' + b' = 4.

  • 2a' + b' = 5 , 5a' + 2b' = 36 : a' = 26 incompatible avec 2a' + b' = 4

  • 2a' + b' = 9 , 5a' + 2b' = 20 : a' = 2 , b' = 9 - 4 = 5 : pgcd(a',b') = 1. La solution est  a = 6, b = 15.

11.  Rechercher les entiers a et b tels que pgcd(a,b) = a - b  (niveau TerS Spé Math / Sup).

12.  Recherche du PGCD de deux entiers : a = n3 - n2 - 12n  et  b = 2n2 - 7n - 4  (niveau TerS Spé Math / Sup).

 ➔  Pour en savoir plus :

© Serge Mehl - www.chronomath.com