ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Algorithme d'Euclide pour le PGCD
      » Notion d'algorithme ,  programme , variante par différences , programme sur Tableur , programme récursif

Soit à rechercher le PGCD, noté a ^ b, de deux entiers naturels (non nuls) a et b.

a ^ b = b ^ r

ce qui montre que l'algorithme d'Euclide est récursif. On aura alors, en notant rk les restes des divisions successives : de a par b (reste = r = r1), b par r1 (reste = r2), r1 par r2 (reste = r3), ...  :

a ^ b = b ^ r1 = r1 ^ r2 = r2 ^ r3 = ...

En constatant que la suite (rn) ainsi définie des restes des divisions successives est une suite strictement décroissante dans N, majorée par 0, il existe donc un entier n pour lequel on a rn = 0. On déduit du cas a multiple de b que a ^ b = rn-1 : dernier reste non nul des divisions successives.

Programmation Javascript de la méthode :

Ce programme affiche les résultats des divisions euclidiennes successives et, par défaut, 24 et 18 sont entrés ci-dessous dans a et b. Remarquer que le programme reste valide si a < b : on aura une ligne supplémentaire de calcul qui nous restituera le "bon" cas a > b. Ce programme peut calculer le PPMC de a et b (plus petit multiple commun, dit aussi PPCM...). Il suffit d'appliquer la formule "bien connue" :

ab = PGDC(a,b) × PPMC(a,b)

 ➔    Code HTML du formulaire permettant de lancer les calculs à la demande est

<INPUT TYPE=button NAME=Bouton VALUE="Lancer le programme" onclick="pgcd()">

<SCRIPT LANGUAGE=JavaScript>

function pgcd()
{
a=24 ; a=prompt("a = ",a)
if (a==null) {return} else {a=eval(a)}
b=18 ; b=prompt("b = ",b)
if (b==null) {return} else {b=eval(b)}
a0=a ; b0=b
wdow=open("","calculs","height=650,width=450","scrollbars=yes");
wdow.document.write("<PRE>");
while (b > 0)
{
r = a % b ;
wdow.document.writeln("a="+a+"\tb="+b+"\tq="+(a-r)/b+"\tr="+r);
a = b ; b = r;
}
wdow.document.writeln("")
wdow.document.writeln("PGCD("+a0+" , "+b0+") = "+a)
return
}
</SCRIPT>

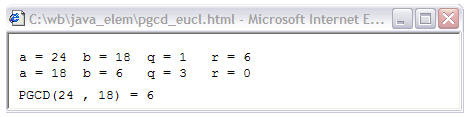
Exemples d'exécution :     

1.  a = 24 et b = 18

2.  a = 12345678910111213  b = 10000000000000007

  Ce résultat est aberrant : le programme fournit 36 alors que les nombres donnés sont impairs... De même, l'équivalent sur tableur place des 0 au-delà de 15 chiffres significatifs. L'examen des calculs montre que l'ordinateur a saisi :

a = 12345678910111212 , b = 100000000000000008

entiers effectivement divisibles par 36 : fantaisies dues à un dépassement de capacité non signalé (plus de 15 chiffres significatifs).

Calcul du « bon » PGCD : »PGCD par différences :  »               Nombres premiers : »
© Serge Mehl - www.chronomath.com