ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

RAMANUJAN Srinivasa Aaiyangar, indien, 1887-1920        » Inde , Prix Sastra Ramanujan

Passionné dès le plus jeune âge par les mathématiques, Srinivasa Ramanujan commence une carrière de greffier (préposé aux archives des tribunaux) tout en s'adonnant seul à sa matière de prédilection au détriment d'études universitaires conventionnelles.

Il découvre (ou retrouve), principalement en arithmétique et en analyse numérique où il s'avère un prodigieux calculateur, des résultats remarquables (développements en série, développement en fractions continues de nombres transcendants, solutions d'équations diophantiennes, ...) dont les démonstrations, lorsqu'il les donne, font preuve d'une géniale intuition, même si elles ne sont pas toujours correctes. Son approche en arithmétique rappelle celle du non moins génial Pierre de Fermat.

L'Inde est alors aux mains des Anglais (depuis le milieu du 18è siècle, elle obtient son indépendance en 1947). Ramanujan se tourne vers l'Angleterre pour faire connaître ses travaux : il écrit à plusieurs mathématiciens anglais en leur faisant part de ses découvertes. Travaillant sur les mêmes sujets au Trinity College de Cambridge, Godefroy Hardy est très impressionné. Il l'invite à le rejoindre en 1914.

Commence alors une collaboration fructueuse en théorie des nombres avec Hardy. Ces deux derniers lui accorderont l'équivalent d'un doctorat (1916) suite à ses recherches sur la décomposition en facteurs premiers des grands nombres (les Highly composite numbers, sujet important aujourd'hui pour le cryptage des données). Grace à l'appui de Hardy et Littlewood, les travaux de Ramanujan furent reconnus par la Royal Society : il y fut élu en 1918. Mais sa santé, déjà chancelante avant son départ vers l'Angleterre, s'est gravement dégradée.

Un triste destin pour ce mathématicien aujourd'hui reconnu comme un génie : les médecins militaires qui occupaient une partie de l'université transformée en hôpital durant la guerre diagnostiquent la tuberculose. Il retourne en Inde en 1919 où il retrouve son épouse (22 ans) délaissée depuis 5 années. Il meurt l'année suivante. L'ensemble des résultats, fruits de son travail conjoint avec Hardy, augmenté de notes posthumes du jeune mathématicien ne seront publiés qu'en 1927 par Hardy et l'université de Cambridge sous le nom de Collected papers of Srinivasa Ramanujan.

En théorie des nombres, dans le cadre des propriétés de factorisation et divisibilité des entiers naturels, Ramanujan définit la notion de nombre hautement composé (Highly composite numbers, 1915, » réf.1, en abrégé NHC) pour signifier qu'un tel nombre possède plus de diviseurs que tout entier non nul qui lui est inférieur. C'est en quelque sorte le concept antinomique des nombres premiers.

Autrement dit, d(n) désignant le nombre de diviseurs d'un entier naturel n :

n est hautement composé   ⇔   ∀ k∈ N* : k< n ⇒ d(k) < d(n)

On peut, par convention, considérer 1 comme hautement composé. Nous ne le ferons pas ici.

• 2 , 4 = 2² son hautement composés;

• 6 = 2 × 3 possède 4 diviseurs : 1, 2, 3 et 6; donc d(6) = 4 et pour tout k = 1, 2, 3, 4 , 5, d(k) < 4. 6 est NHC.

• 15 = 3 × 5 n'est pas NHC : il possède 4 diviseurs alors que 12, par exemple, en possède 6 : 1, 2, 3, 4, 6, 12.

Rappelons que si n = p₁^αp₂^β ... p_k^γ est la décomposition en produit de facteurs premiers d'un entier n non premier, son nombre de diviseurs (y compris 1 et lui même) est le produit : (α+1)(β+1)...(γ+1).

Multiples et diviseurs d'un entier naturel :  »

Proposition 1 :   

Tout nombre hautement composé est pair

Preuve : soit n supposé impair et NHC. Sa décomposition en produit de facteurs premiers est de la forme n =  p₁^α p₂^β ... p_k^γ avec p₁ ≥ 3. Considérons alors l'entier n' =  2^α × p₂^β ... p_k^γ. Ce nombre a autant de diviseurs que n, à savoir (α+1)(β+1)...(γ+1) comme rappelé ci-dessus et n' < n. Contradiction eu égard au statut NHC de n.

Outre 2, 4 et 6, les premiers nombres hautement composés inférieurs à mille sont (pour une liste plus étoffée, » réf.7) :

• 12 = 2² × 3 , 24 = 2³ × 3 , 36 = 2² × 3², 48 = 2⁴ × 3 , 60 = 2³ × 3 × 5 , 120 = 2³ × 3 × 5 , 180 = 2² × 3² × 5

• 240 = 2⁴ × 3 × 5 , 360 = 2³ × 3² × 5 , 720 = 2⁴ × 3² × 5 , 840 = 2³ × 3 × 5 × 7 , ...

Proposition 2 :   

La décomposition en facteurs premiers de tout NHC n possédant k facteurs premiers peut s'écrire sous la forme :

n =  2^α1 ×  3^α2 × 5^α3 ×  ...  × p_k^αk           » réf.8

où p_k désigne le k-ème nombre premier (2 = p₁, 3 = p₂, ...), de sorte que α1 ≥  α2 ≥  α3 ≥ ... ≥ αk
avec αk = 1 sauf pour n = 4 et n = 36 auquel cas αk = 2

Proposition 3 :   

L'ensemble des nombres hautement composés est infini

Preuve : soit un NHC n. Pour tout k< n, on a d(k) < d(n). Considérons le nombre 2n. Ce nombre possède les diviseurs de n et 2n lui-même, donc d(2n) > d(n) > d(k) pour tout k < n; il est donc candidat à être le prochain nombre hautement composé supérieur à n dans l'intervalle ]n + 2,2n - 2[ de N. Ce sera le cas si les nombres n + 2, n + 4, ... 2n - 2 ont moins de diviseurs que 2n.

Proposition 4 :   

Tout nombre hautement composé supérieur à 6 est abondant    (» nombres abondants)

Proposition 5 :   

Tout nombre hautement composé est un nombre pratique    (» nombres pratiques)

Mais c'est quoi un nombre pratique ?  »

Il s'agit du célèbre (dans le monde mathématique...) nombre, exponentielle de e^π√163, rencontré par Ramanujan dans des calculs relatifs à des approximations du nombre π, (Modular Equations and Approximations to π, 1912).

Ce nombre, que l'on rencontre dans l'étude de certaines fonctions, fut prétendu entier d'autant que le regretté Martin Gardner, mathématicien et malicieux, s'était ingénié à le faire croire en 1975 :

e^π√163 = 262 537 412 640 768 744 ?

En fait, ce nombre est transcendant et on sait, grâce aux progrès des calculateurs électroniques, qu'on a sensiblement :

e^π√163 = 262 537 412 640 768 744,99999999999925

L'égalité x² + 7 = 2ⁿ , x∈N, n∈N, n'est possible que pour n = 3, 4, 5, 7 ou 15

Cette conjecture ne fut prouvée que relativement récemment (en 1960) par le mathématicien norvégien Nagell Trygve, en travaillant dans l’extension de corps Q(√-7).

 i  Trygve Nagell (1895-1988) : mathématicien norvégien qui étudia à l'université d'Oslo. Spécialiste en géométrie algébrique et théorie des nombres, il enseigna principalement à l'université d'Upsal (Uppsala, Suède). Pour en savoir plus, on pourra consulter la page Wikipedia consacrée à ce mathématicien. On ne le confondra pas avec le mathématicien allemand Christian Nagel (1821-1903).

∗∗∗
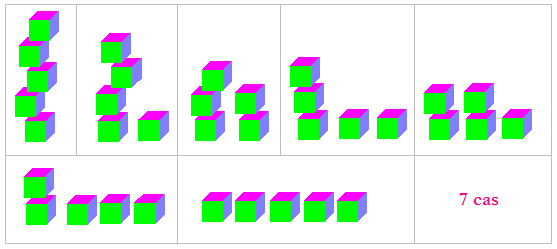
Vous avez n cubes identiques. De combien façons peut-on les grouper ?

si n = 3, on a 3 possibilités :

si n = 4, on a 5 possibilités :

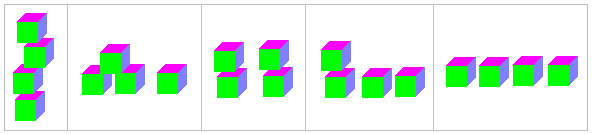
si n = 5, on a ? possibilités :

  ?     ?   » Réponse

De façon moins ludique :

Combien un entier naturel n admet-il de décompositions en sommes d'entiers non nuls ?

• n = 4 = 3 + 1 = 2 + 2 = 2 + 1 + 1 = 1 + 1 + 1 + 1

• n = 5 = 4 + 1 = 3 + 2 = 3 + 1 + 1 = 2 + 2 + 1 = 2 + 1 + 1 + 1 = 1 + 1 + 1 + 1 + 1

• n = 8 = 7 + 1 = 6 + 2 = 5 + 3 = 4 + 4 = ... pourriez-vous trouver les 17 autres décompositions ?

Le cas général est très compliqué; Polya et Rademacher en donnèrent la solution : la formule est  abominable... (» réf.9-11) Ramanujan en trouva indépendamment une approximation relativement simple : si on appelle g(n) le nombre des groupements de n cubes, on a :

       (source : J. conway, Le livre des nombres)

Partitions d'un entier naturel, formule de récurrence et programmation : »        Nombres Taxicab : »

• Dans la catégorie des nombres presque entiers, on a le très joli :

  e^π - π = 19,9990999... , soit e^π - π = 20 à 10^-3 près !
   

• Concernant ses recherches sur le nombre π, on doit à Ramanujan cette approximation irrationnelle :

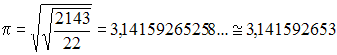
Cette formule frôle donc π à près de 10^-9 près...

Calculs de π dans ChronoMath (programmes JavaScript "on line") : »

• 1729 est le plus petit entier se décomposant de deux façons en la somme de deux cubes, à savoir 12³ + 1³ et 10³ + 9³.
  Noter que 1729 = 7 × 13 × 19 est aussi un nombre (le troisième) de Carmichael.
   

• Un développement en fraction continue :

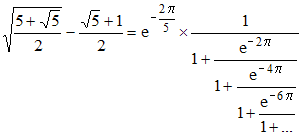
∗∗∗ Élèves de Terminale :  sans chercher à prouver cette jolie formule..., contrôlez votre aptitude à vous servir de la calculatrice. Vous devriez trouver, en vous limitant au développement indiqué et en limitant le dernier terme affiché, 1 + e^-6π/(1 + ...) à 1 + e^-6π, que les deux membres sont égaux à 0,2840790438 (à 10^-11 près). La convergence est rapide : on peut le vérifier grâce à l'inégalité de Legendre,

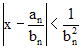
Longueur de l'ellipse selon Ramanujan : »

Ce prix fut instauré en 2005 par L'Académie des Arts, des Sciences, de la Technologie et de la Recherche de l'université de Shanmugha (SASTRA), sise au sud de l'Inde. D'un montant de 10000$, il est décerné chaque année à un jeune mathématicien dont l'âge n'excède pas 32 ans pour ses contributions exceptionnelles dans les domaines de recherches mathématiques de Srinivasa Ramanujan. Le prix sera décerné chaque fin décembre lors d'une conférence internationale organisée par SASTRA à Kumbakonam, ville natale de Ramanujan, décédé fin décembre à 32 ans.
Source : https://web.archive.org/web/20070417045544/http://www.math.ufl.edu/sastra-prize/

 ➔   Pour en savoir plus :

 Sur les nombres hautement composés :

1. Highly composite numbers, par S. Ramanujan (So. math. de Londres, 1915), annotations de Jean-Louis Nicolas (1997) :
   http://math.univ-lyon1.fr/~nicolas/ramanujanNR.pdf 

2. Nombres hautement composés (article dédicacé à Paul Erdös) par Jean-Louis Nicolas, univ. Claude Bernard, Lyon (1988) :
   http://math.univ-lyon1.fr/~nicolas/composeAA.pdf

3. Répartition des nombres hautement composés de Ramanujan, par Jean-Louis Nicolas, univ. Claude Bernard, Lyon (1970) :
   http://www.numdam.org/article/STNB_1969-1970____A13_0.pdf

4. Highly composite number : https://en.wikipedia.org/wiki/Highly_composite_number

5. Highly composite numbers sur The on-line encyclopedia of integer sequences : https://oeis.org/A002182

6. On highly composite numbers, par Paul Erdös, 1944 (retour sur un résultat de Ramanujan relatif au nombre de nombres
   hautement composés inférieurs à un entier donné) : https://users.renyi.hu/~p_erdos/1944-04.pdf

7. The on-line encyclopedia of integer sequences : https://oeis.org/A002182

8. Autour des diviseurs d'un entier, ch. 1, pages 7 et suivantes; preuve proposition 2 : pages 16 et suivantes :
   http://www.univers-ti-nspire.fr/files/pdf/01-arith-diviseurs-TNS21.pdf

 Sur le nombre de partitions d'un entier naturel :

9. De Ramanujan à Hardy, de la première à la dernière lettre, par Don Zagier (revue Tangente, HS n°25) :
   https://people.mpim-bonn.mpg.de/zagier/files/scanned/RamanujanTangente/RamanujanTangente.pdf

10. Nombres de partitions sur OEIS : https://oeis.org/A000041

11. The Hardy-Ramanujan Asymptotic Partition formula :
    https://www.theoremoftheday.org/NumberTheory/Partitions/TotDPartitions.pdf

Autres :

12. Nombres superabondants (étudiés par Paul Erdös et J.-L.Nicolas) :
    http://math.univ-lyon1.fr/~nicolas/erdosSA.pdf

13. Congruences et formes modulaires, par Jean-Pierre Serre (séminaire bourbali, 1971) :
    http://www.numdam.org/article/SB_1971-1972__14__319_0.pdf

14. Published papers & unpublished Notebooks : http://ramanujan.sirinudi.org/

15. Sur des travaux non publiés de S. Ramanujan, par G. Robin (1990) :
    http://math.univ-lyon1.fr/~nicolas/robinRamanujan.pdf

16. » Collected papers of Srinivasa Ramanujan est en vente sur Amazon : https://amzn.to/2PX0JEa.
    La biographie de Ramanujan par Godefroy Hardy, la liste des 37 sujets étudiés et de nombreuses pages sont en lecture libre.

17. Visitez la page d'Eric Weisstein relatives aux Almost integer.

     

---

Radon   Skolem

---

© Serge Mehl - www.chronomath.com

       

 
 

---

© Serge Mehl - www.chronomath.com