
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

 Don Zagier étudia
les mathématiques et la physique aux États-Unis avant de revenir en Allemagne où
il complète son
doctorat (1972) à l'université de Bonn sous la direction de
Hirzebruch portant sur les classes
équivariantes de Pontriaguine (algèbre homologique) en lien avec la théorie
des nombres (il a alors à peine plus de 20 ans).
Don Zagier étudia
les mathématiques et la physique aux États-Unis avant de revenir en Allemagne où
il complète son
doctorat (1972) à l'université de Bonn sous la direction de
Hirzebruch portant sur les classes
équivariantes de Pontriaguine (algèbre homologique) en lien avec la théorie
des nombres (il a alors à peine plus de 20 ans).
Professeur à Bonn, il obtient en 1979, une chaire de théorie des nombres à l'université du Maryland (USA) qu'il conserve jusqu'en 1990. Don Zagier reçut le prix Cole 1987. Membre de l'Institut Max Planck pour les mathématiques (MPIM) depuis 1984, il en est le codirecteur, avec Gerd Faltings, depuis 1995.
Outre des postes au Japon, en Italie et aux Pays-Bas, Zagier professa au collège de France de 2001 à 2014. Récipiendaire du prix von Staudt 2001, Don Zagier revisite les travaux de Ramanujan en théorie des nombres (» réf.8). Ses recherches le conduisent à l'étude des formes modulaires et à des applications inattendues en physique théorique (théorie des cordes, trous noirs, ...).
S'intéressant à des travaux de Diophante sur les nombres congruents ainsi dénommés pour signifier un entier naturel A sans facteur carré tel qu'il existe un rectangle à côtés rationnels d'aire A, Don Zagier a prouvé le résultat suivant (» réf.2) :
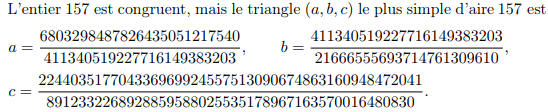
En savoir un peu plus sur les nombres congruents : »
En 1997, on lui doit la republication dans la revue American Mathematical Monthly, de la preuve (4 pages) du théorème des nombres premiers, Simple analytic proof of the prime number theorem, publiée en 1980 par le mathématicien américain Donald J. Newman dans ladite revue. Une preuve, tout comme celle de Selberg et Erdös en 1948-49, ne faisant pas appel à l'analyse complexe (» réf.5).
i Donald J. Newman : mathématicien américain (1930-2007), spécialiste en théorie des nombres, analyse complexe et en théorie de l'approximation polynomiale, sujet de sa thèse, Some aspects of polynomial approximation (univ. Harvard, 1958). Il fut professeur dans de nombreuses universités américaines dont le MIT (Massachusetts Institute of Technology) où il rencontra John Nash qui devint son ami.
➔ Pour en savoir plus :
Congruences et formes
modulaires, par Jean-Pierre Serre
(séminaire bourbali, 1971) :
http://www.numdam.org/article/SB_1971-1972__14__319_0.pdf
Le problème des nombres congruents,
formes modulaires, par
Pierre Colmez (École polytechnique) :
https://webusers.imj-prg.fr/~pierre.colmez/congruents.pdf
De Ramanujan à Hardy, de la première à la dernière
lettre, par Don Zagier (revue Tangente, HS n°25) :
https://people.mpim-bonn.mpg.de/zagier/files/scanned/RamanujanTangente/RamanujanTangente.pdf
Institut Max Planck pour les mathématiques : http://www.mpim-bonn.mpg.de/
Newman's short proof of the prime number theorem :
https://www.math.fsu.edu/~quine/ANT/ZagierOnNewman.pdf
ou bien :
https://people.mpim-bonn.mpg.de/zagier/files/doi/10.2307/2975232/fulltext.pdf
Preuve selon Zagier du théorème des deux carrés de Fermat selon lequel si p est premier congru à 1 modulo 4, alors p est somme de deux carrés.