
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges


Sources biographiques : Larousse du 20è siècle en 6 volumes (tome 4, 1931) et réf.1
Natif d'Amiens, normalien (ancien élève de l'École normale supérieure), il fut attaché dès sa sortie à l'Observatoire de Paris auprès de Le Verrier (1864) puis professeur de mathématiques en classes préparatoires, en particulier à Moulins, puis Paris aux déjà renommés lycées Charlemagne et lycée Saint-Louis. On lui doit également des conférences aux Collège de France. Il meurt à l'âge de 49 ans des suites d'une infection généralisée due à une blessure accidentelle au visage lors d'un congrès à Marseille.
Ses travaux portent :
• Sur la géométrie supérieure : entendant là le terme du 19è siècle relatif à la géométrie euclidienne non élémentaire, c'est à dire celle qui émergea avec l'étude des transformations (homothéties, similitudes, inversion) et, tout particulièrement, la géométrie projective avec ses transformations homographiques et homologiques.
• Sur l'arithmétique de Diophante et plus généralement sur la Théorie des nombres dont seul le premier tome de son traité fut publié l'année de sa mort sous cette appellation en 1891 (Éd. Gauthier-Villars, » réf.2). Dans ce contexte arithmétique, il découvrit (1876) le 12è nombre de Mersenne M127 = 2127 - 1. Un record à une époque où les recherches se faisaient encore "à la main" !
| La formule d'Euler-Descartes : |
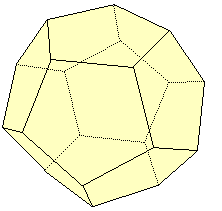
On doit à Édouard Lucas une belle et simple preuve de la formule d'Euler-Descartes liant le nombre de sommets (S), de faces (F) et d'arêtes (A) d'un polyèdre convexe :
| Nombres de Lucas : |
Ces nombres interviennent dans la résolution d'équations diophantiennes : ils vérifient la relation de récurrence :
Les premiers nombres de Lucas sont 1, 3, 4, 7, 11, 1, 29, 47, 76, ... ils vérifient la relation de récurrence :
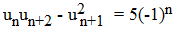
Calcul JavaScript des nombres de Lucas : » Suite de Fibonacci : »
| Lucas et les nombres premiers de Mersenne : |
Lucas étudia la primarité (ou primalité, de l'anglais primality) des nombres de Mersenne, de la forme Mn = 2n - 1 , n entier naturel premier, et énonça (1876) une condition de primarité de ces nombres conduisant à la découverte récente, grâce aux ordinateurs de nombres premiers Mn gigantesques.
Grâce à ce test, Lucas découvrit les nombres de Mersenne premiers jusqu'à n = 127. Ce n'était pas une mince affaire car à cette époque (1876), il n'y avait ni ordinateurs ni machines à calculer capables de traiter d'aussi grands nombres :
M127 = 2127 - 1 = 170141183460469231731687303715884105727 (39 chiffres)
Les tout derniers nombres de Mersenne : » Critère de Lucas-Lehmer : » » Carmichael
| Les célèbres tours de Hanoi : |

Dans ses Récréations mathématiques, publiées à partir de 1882, Lucas introduit les célèbres tours de Hanoi : On se donne trois tiges verticales. Sur la première sont empilés des anneaux de diamètres distincts du plus grand au plus petit. Le jeu consiste à déplacer ces anneaux sur la dernière « tour » en un minimum de coups, la tour centrale servant d'intermédiaire et en respectant toujours la règle suivante :
Aucun disque ne doit être placé sur un disque de rayon inférieur
Ce jeu est très difficile dès que l'on dépasse 4 anneaux car on peut démontrer qu'il se joue en 2n - 1 coups, n désignant le nombre d'anneaux : c'est l'objet de l'exercice ci-après.
∗∗∗
Exercice (niveau
1ère ES) : on considère les suite (un)
et (vn) définies par u1 = 1 , un = 2un-1
+ 1 et vn = un + 1
Soit wn le nombre minimal de déplacements de disques conduisant à la solution des tours de Hanoi dans un jeu à n disques. En utilisant la 3è tour comme tour intermédiaire, on peut déplacer les (n-1) disques supérieurs sur la seconde tour en wn-1 coups.
Le n-ème disque (le plus large) peut alors être placé sur la 3è; reste à déplacer les (n-1) disques présents sur la seconde tour vers la 3ème en utilisant la 1ère tour comme intermédiaire (sans jamais toucher au n-ème disque !!) : cela se fera au mieux en wn-1 coups.
En déduire que les suites (un) et (wn) coïncident. Conclure.
» On voit là un algorithme permettant de passer d'une solution connue à n disques à la solution pour (n+1) disques.
| Carré diabolique également dit carré cabalistique : |
Toujours dans le cadre ludique mais relevant cependant de la théorie additive des nombres, on doit à Lucas le concept et la construction de carrés diaboliques : on nomme ainsi un carré magique normal qui le reste malgré toute permutation circulaire sur ses lignes ou ses colonnes.
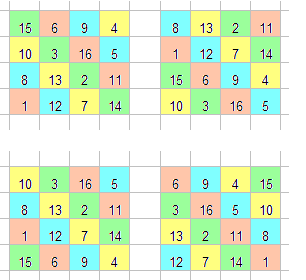
Cela revient à dire que les sommes de 4 termes obtenues sur des diagonales secondaires parallèles (une ligne ou colonne n'étant utilisée qu'une seule fois dans le choix des termes) est égale à la constante du carré. Ces termes sont indiqués ci-contre dans une même couleur. La constante de ce carré magique d'ordre 4 est 34.
➔ Pour en savoir plus :
Théorie des nombres d'Edouard Lucas (1891), sur Gallica
(Bibliothèque nationale de France) :
http://gallica.bnf.fr/ark:/12148/bpt6k29021h.table
Récréations mathématiques d'Edouard Lucas, sur Gallica :
http://gallica.bnf.fr/ark:/12148/bpt6k3943s
dont :
- le problème du
batelier (le loup, la chèvre et le chou)
et sa généralisation à n couples
de
maris jaloux...
- le problème des 8 reines,
le problème des ménages, les 7 ponts de
Königsberg,
le jeu du solitaire, etc.
Second volume : http://gallica.bnf.fr/ark:/12148/bpt6k39443.r=Récréations+mathématiques+Lucas.langFR
Troisième volume 3 (dont les Tours de Hanoï) :
http://gallica.bnf.fr/ark:/12148/bpt6k3945d.r=Récréations+mathématiques+Lucas.langFR