
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Ancien élève de l'École Normale supérieure, agrégé de mathématiques, professeur de mathématiques spéciales à Poitiers, Mont-de-Marsan et au lycée Charlemagne (Paris). Ami de Lucas et de Hermite avec lesquels il collabore sur de nombreux sujets dans diverses publications : théorie des nombres, intégrales eulériennes, courbes algébriques.
De Longchamps fonda (1880) une revue réputée : le Journal de Mathématiques spéciales dans laquelle il publia nombre de ses recherches, à distinguer du Journal de Mathématiques élémentaires (1876) et de la Revue de Mathématiques spéciales (1890), édités par les éditions H. Vuibert. Ci-dessous, un extrait d'un article de Gohierre de Longchamps relatif à la trisectrice de Maclaurin :
On doit à Gohierre de Longchamps la paternité de nombreuses courbes planes définies géométriquement et appellations s'y rattachant (lieux géométriques dits, depuis les années 1970, ensemble de points).
Un autre exemple, le bicorne : »
Par ailleurs, la fin du 19è siècle montre un intérêt immodéré pour la géométrie du triangle, principalement à l'usage des élèves de mathématiques supérieures et spéciales. Gohierre de Longchamps a ainsi donné son nom à de nombreux résultats sur le sujet. En particulier :
| Cercle de (de) Longchamps : |
Soit un triangle ABC; traçons les cercles (a), (b) et (c), de centres respectifs A, B et C et dont les rayons sont les mesures des côtés opposés. Si le centre radical ω de ces cercles existe et leur est extérieur, alors il existe un cercle orthogonal à ces trois cercles appelé cercle de Longchamps; son centre est ω, dit point de Longchamps, symétrique de l'orthocentre H par rapport au centre O du cercle circonscrit au triangle ABC.
Ce cercle passe par les points de contact des tangentes issues de ω aux trois cercles (a), (b), (c); son rayon est le diamètre du cercle polaire du triangle ABC.
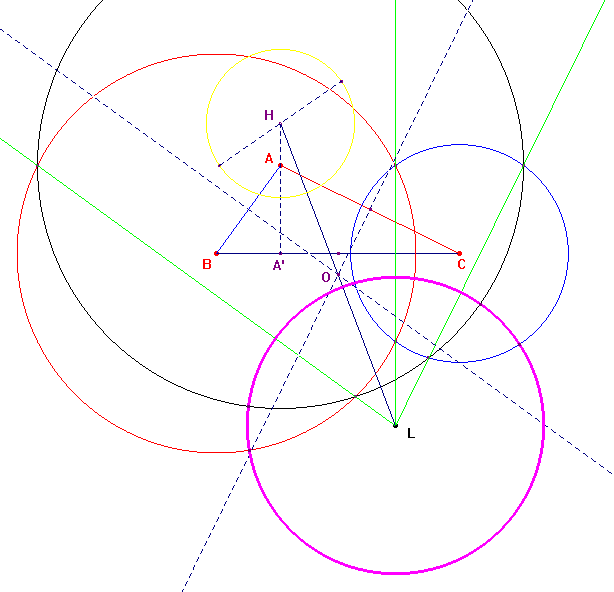
➔ Rappelons que l'axe radical de deux cercles est la droite, ensemble des points ayant même puissance par rapport à ces deux cercles. Étant donné trois cercles, le centre radical ω, s'il existe, est le point d'intersection des axes radicaux des cercles pris deux à deux.
Les trois segments de tangente que l'on peut mener de ω à ces trois cercles ont même mesure : c'est le rayon du cercle radical. Le cercle de Longchamps est également orthogonal aux cercles centrés en les pieds des médianes ayant pour rayons les médianes correspondantes.
| Trisectrice de (de) Longchamps : |
C'est un cas particulier d'épispirale, inverse de pôle O d'une rosace de Grandi qui serait ici un simple trifolium. Son équation polaire est de la forme r = a/cos3t.

la courbe r = 2/cos3t vue par
GraphMathica
Les asymptotes ont pour équation y = ± x/√3 et x = -2/3. Pour cette dernière, obtenue lorsque t = 3π/2, y est infini mais x = r.cost = 2cost/cos3t = 2/(4cos2t - 3) → -2/3.
La courbe r = a/cos(3t) étant tracée dans le 1er quadrant, soit M un de ses points d'angle polaire t. Traçons le cercle de rayon a et la tangente [OT) comme illustrés ci-dessous.
Le triangle OMT est rectangle en T; on a : MT = OM × cos^OMT, soit a = a/cos(3t) x cos^OMT. C'est dire que ^OMT = 3t. Ainsi, un angle de mesure α étant donné (inférieur à 90°), on place un gabarit triangulaire droit OMT tel que ^OMT = α et MT = a, O à l'origine, M sur la courbe. L'angle ^xOM réalise alors la trisection de α.
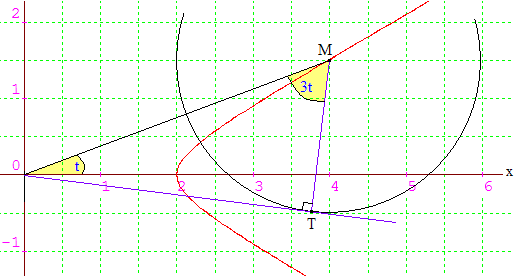
➔ En écrivant que cos3t = ar, soit 4cos3t - 3cost = a/r, c'est à dire 4x3/r3 = (3x + a)/r vu que x = r.cost et x2 + y2 = r2, on obtient l'équation cartésienne de la trisectrice. C'est une cubique :
4x3 - (x2 + y2)(3x + a) = 0
On peut alors facilement exprimer y en fonction de x :
![]()
Enfin, la courbe est également unicursale (elle admet une représentation paramétrée) : on a y/x = tan t; on pose alors tan t = u; sachant que dans ce changement de variable 1/cos2t = 1 + tan2t = 1 + u2, on a immédiatement :
![]()
| Un calcul de π : |
Dans un article publié dans les annales de l'ÉNS, Sur les intégrales eulériennes de seconde espèce (1880), G. de Longchamps exhibe un calcul de π/2 :
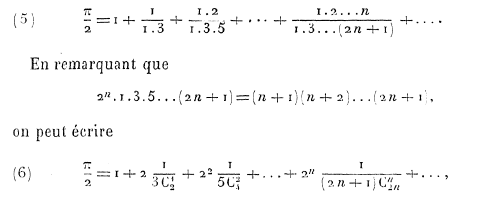
|
Programmation de l'algorithme en JavaScript : |
Entrez nmax au moins (par défaut 100). Quelques résultats produits par le programme :
! Notons que l'absence, dans le programme, de critères relatifs au contrôle d'erreurs d'arrondis nuit à la crédibilité des calculs. Facile de calculer π quand on connaît déjà sa valeur à 10-n près, n quasiment arbitrairement grand...
|
<SCRIPT LANGUAGE=JavaScript> { </SCRIPT> |
| Autres travaux : |
En arithmétique, G. de Longchamps étudia la primarité (ou primalité en franglais) des nombres de la forme 2n ± 1 par une décomposition en base 2 dont on trouvera l'étude sur le site Gallica de la BNF (réf.3) :
➔ Pour en savoir plus :