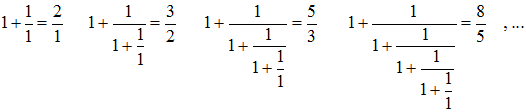ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
 |
Rappelons le célèbre petit problème de Fibonacci : possédant au départ un couple de lapins, combien de couples de lapins obtient-on en douze mois si chaque couple engendre tous les mois un nouveau couple à compter du second mois de son existence ? |
 |
Notons un le nombre de couples de lapins au mois n. Dès le début du troisième mois, nos lapins ont deux mois et ils enfantent un couple de lapins : u3 = 2.
Plaçons-nous au n-ème mois (n > 1) et cherchons à exprimer ce qu'il en sera au (n+1)-ème mois : un+1 est la somme des couples de lapins au mois n et des couples nouvellement engendrés.
Or, seuls les couples nés deux mois auparavant engendrent au mois n+1. On a donc :
un+1 = un + un-1
La suite est manifestement strictement croissante et divergente. L'étude des suites récurrentes à deux termes permet d'écrire ici :
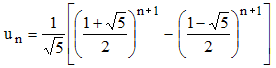 Formule
de Binet pour la suite de Fibonacci :
»
Formule
de Binet pour la suite de Fibonacci :
»
On reconnaît là le trop fameux nombre Φ = (1 + √5)/2 et la section dorée = (√5 - 1)/2, son inverse, inférieure à 1. Pour n tendant vers l'infini, cette seconde parenthèse tend vers 0. On en déduit que la suite (qn) des rapports un/un-1 tend donc vers Φ et celle des rapports un/un-2 tend donc vers Φ2.
On peut écrire un petit programme récursif conduisant au calcul des éléments de la suite (un) suite mais, tout comme pour la fonction d'Ackermann, l'ordinateur sature rapidement car il doit empiler les résultats partiels successifs tant que la condition d'arrêt n'est pas atteinte :
Calcul JavaScript récursif des nombres de Fibonacci : »
Au moyen d'un tableur, il est facile d'écrire un programme utilisant la recopie vers le bas, calculant les termes successifs et les rapports un/un-1 notés qn :
| A | B | C | D | |
|---|---|---|---|---|
| 1 | n | u(n) | u(n-1) | q(n) |
| 2 | 1 | 1 | 1 | 1 |
| 3 | =A2+1 | =B2+C2 | =B2 | =B3/C3 |
| 4 | =A3+1 | =B3+C3 | =B3 | =B4/C4 |
| 5 | recopier vers le bas | recopier vers le bas | recopier vers le bas | recopier vers le bas |
On obtient :
|
|
|
|
|
|
|
1 |
n | u(n) | u(n-1) | q(n) |
|
2 |
1 | 1 | 1 | 1 |
|
3 |
2 | 2 | 1 | 2 |
|
4 |
3 | 3 | 2 | 1,5 |
|
5 |
4 | 5 | 3 | 1,666666667 |
|
6 |
5 | 8 | 5 | 1,6 |
|
7 |
6 | 13 | 8 | 1,625 |
|
... |
... ... | |||
|
11 |
10 | 89 | 55 | 1,618181818 |
|
12 |
11 | 144 | 89 | 1,617977528 |
|
13 |
12 | 233 | 144 | 1,618055556 |
|
... |
... ... | |||
|
20 |
19 | 6765 | 4181 | 1,618033963 |
Ces calculs nous conduisent à autre preuve de convergence de la suite (qn). On constate une convergence probable des qn vers 1,618 environ (voir ci-après). Prouvons cela :
Par définition de la suite (un), on déduit :
En posant G(x) =1 + 1/x, on a qn+1 = G(qn). La fonction G s'étudie facilement : elle applique l'intervalle J = [3/2, 2] dans J et admet, dans cet intervalle un unique point fixe Φ = (1+√5)/2, solution positive de l'équation x = 1 + 1/x se ramenant à x2 - x - 1 = 0.
On a qn+1 = G(qn) et, sur le voisinage J de Φ, la fonction dérivée G' de G, à savoir G'(x) = -1/x2 vérifie la double inégalité :
0 < | G'(x) | < 4/9 < 1
En vertu du critère du point fixe, la suite (qn) converge et sa limite Φ > 0 vérifie donc G(Φ) = Φ, soit :
Φ = 1 + 1/Φ, ce qui peut s'écrire : Φ2 - Φ - 1 = 0 , Φ = 1,618034 à 10-6 près
On a reconnu le nombre d'or...
| Remarques : |
L'égalité Φ2 - Φ - 1, peut s'écrire :
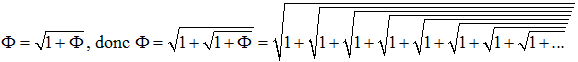
➔ On peut aussi s'intéresser à la fraction continue :
 s'écrivant sous forme fractionnaire :
s'écrivant sous forme fractionnaire :
C'est encore le nombre d'or car ce nombre vérifie manifestement : F = 1 + 1/F. On remarquera que les réduites successives ne sont autres que les un+1/un :