
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
|
Notations & symboles : qui ? » Appellations & concepts |

|
Notations & symboles : qui ? » Appellations & concepts |
à strictement parler, la réponse à cette question pourrait être aucun ! L'origine d'un concept ou d'une appellation est souvent ambiguë car la mathématique, dans chacun de ses aspects, ne fut pas, n'est pas, l'œuvre d'un seul. Les noms cités correspondent à l'acceptation définitive, par la communauté mathématique, de la notation ou du concept.

Q : ensemble des nombres rationnels :
Bourbaki ? cet ensemble s'identifie aux
fractions,
soit à Z ×
N*
! l'information selon laquelle
Peano serait
à l'origine de cette notation semble fausse.
Peano utilisa
N pour les entiers naturels, R pour les rationnels et Q
pour les réels (quantita)...
En 1948,
Dubreil utilise
Γ
pour nommer Q et Ω
pour nommer C !
»
Variétés algébriques, I, page 5

» Stevin , Argand , Bellavitis , Hamilton, Grassmann , Gibbs » La notation des vecteurs
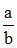 : Oresme
: Oresme( ) : évolution du 16è au
20è ! Dans le but de regrouper des termes, elles apparaissent chez les
algébristes italiens comme Tartaglia
et Cardan.
 i L'usage des
parenthèses en géométrie, pour désigner une droite d : (d), une droite
passant par A et B : (AB), un cercle nommé C : (C), apparaît dans les années
1970 et plus particulièrement dans l'enseignement des mathématiques dites
modernes. Dans les années 1920, Borel parle d'une droite AB, d'un
segment AB (usage des crochets:
voir ci-après), d'un plan P, etc. De même, dans les années 1960 (Lespinard &
Pernet).
i L'usage des
parenthèses en géométrie, pour désigner une droite d : (d), une droite
passant par A et B : (AB), un cercle nommé C : (C), apparaît dans les années
1970 et plus particulièrement dans l'enseignement des mathématiques dites
modernes. Dans les années 1920, Borel parle d'une droite AB, d'un
segment AB (usage des crochets:
voir ci-après), d'un plan P, etc. De même, dans les années 1960 (Lespinard &
Pernet).
On
utilisa beaucoup jusqu'au 18è siècle le surlignage comme![]() pour le produit n(n + 1) ou
pour le produit n(n + 1) ou
![]() pour (a + b)n.
Ce surlignage se rencontre par exemple chez
Vincenzo Riccati,
Stirling,
de Moivre. La barre
pouvait aussi être en dessous, comme le fit Chuquet, avec un usage analogue pour les racines carrées.
pour (a + b)n.
Ce surlignage se rencontre par exemple chez
Vincenzo Riccati,
Stirling,
de Moivre. La barre
pouvait aussi être en dessous, comme le fit Chuquet, avec un usage analogue pour les racines carrées.
La plupart des mathématiciens du 18è siècle, comme
Leibniz,
Euler, les
Bernoulli,
Cramer, utilisèrent un point séparateur,
comme n.n + 1.n + 2 pour n(n + 1)(n + 2).
Leibniz
utilisa aussi n![]() n
+ 1
n
+ 1![]() n + 2,
puis notre notation (a + b)n, mais elle ne
commencera à se généraliser que dans la seconde moitié du 18ème siècle.
n + 2,
puis notre notation (a + b)n, mais elle ne
commencera à se généraliser que dans la seconde moitié du 18ème siècle.![]()
 On voit ainsi, implicitement, par la nécessité d'exhiber
des symboles d'agrégation des termes dans un calcul composé que, pour les
mathématiciens, la multiplication a priorité sur
l'addition (et la soustraction) : a x
b + 1 est a x b augmenté
On voit ainsi, implicitement, par la nécessité d'exhiber
des symboles d'agrégation des termes dans un calcul composé que, pour les
mathématiciens, la multiplication a priorité sur
l'addition (et la soustraction) : a x
b + 1 est a x b augmenté de 1 : la multiplication
s'applique à b , on ajoute ensuite 1. Si l'on veut signifier le produit de
a par b + 1, donc forcer la priorité à l'addition, on
écrivait alors, suivant les auteurs :
de 1 : la multiplication
s'applique à b , on ajoute ensuite 1. Si l'on veut signifier le produit de
a par b + 1, donc forcer la priorité à l'addition, on
écrivait alors, suivant les auteurs :
![]() ,
a
,
a ![]() b + 1, a.b
+ 1, ou comme de nos jours : a(b + 1).
b + 1, a.b
+ 1, ou comme de nos jours : a(b + 1).
!
Collégiens : dans ces conditions, le calcul composé 1 + 2
x 3 est 1 + 6 = 7 et non pas 3
x 3 = 9, résultat faux qu'affichera hélas une
calculette d'écolier comme celle schématisée à droite ! Concernant les
puissances, on a, par exemple, 2 × 32 = 2 × 9 = 18
et non pas 62 = 36. On retiendra que la
puissance l'emporte sur
la multiplication et sur la division , lesquelles
l'emportent sur l'addition et sur la
soustraction.
[ ] : Bombelli utilisa des crochets pour regrouper les termes dans l'écriture de racines cubiques complexes. Les Bernoulli, comme Johann et Daniel généraliseront le rôle des crochets mêlés aux parenthèses (milieu du 18è siècle). Par exemple [1 - (x + 2)2]3, plutôt que (1 - (x + 2)2)3.
➔ En présence de parenthèses (ou crochets), celles-ci (ceux-ci) ont priorité absolue ! Et, en leur absence, si deux opérations ont même priorité (addition & soustraction, multiplication & division), on effectue les opérations dans l'ordre d'écriture :
3 + 4 - 5 = 7 - 5 = 2 → mêmes priorités donc dans l'ordre d'écriture
3 - (4 - 5) = 3 - (-1) = 3 + 1 = 4 → les ( ) sont prioritaires
3 × [4 - (1 - 5)] = 3 × [4 - (-4)] = 3 × [4 + 4] = 3 × 8 = 24 → priorité à la ( ) la plus intérieure, puis au crochet
3 ÷ 4 × 5 = 0,75 × 5 = 3,75 → mêmes priorités donc dans l'ordre d'écriture
et surtout pas 3 ÷ 20 = 0,15 équivalent à 3 ÷ (4 × 5) !
5 × 32 - 1 = 5 × 9 - 1 = 45 - 1 = 44 , (5 × 3)2 - 1 = 152 - 1 = 225 - 1 = 224
9 ÷ 3 + 2 = 3 + 2 = 5 , 9 ÷ (3 + 2) = 9 ÷ 5 = 1,8 , 3 ÷ 4 × 5 = 0,75 × 5 = 3,75
!se calcule avec une calculatrice comme étant 3 ÷ (4 × π) c'est à dire comme 3 ÷ 4 ÷ π dans cet ordre !
i
L'usage des crochets en géométrie est récent : ils
apparaissent chez Bourbaki. pour
désigner un intervalle de la droite
numérique : [a,b], ensemble des nombres réels x tels que a ≤ x ≤ b (a <
b). Puis, timidement, dans les années 1970, on voit apparaître l'intervalle
[A,B], segment de droite géométrique, qui deviendra simplement [AB]. On
distinguera ensuite, dans les années 1980, les droites (AB) et les
demi-droites au moyen de [AB), Tout cela dans le cadre des mathématiques
dites modernes et l'usage de la théorie des ensembles.

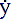 fluxion, équivalent au nombre dérivé :
Newton
fluxion, équivalent au nombre dérivé :
Newton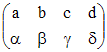 pour une
substitution : Cauchy (1815)
pour une
substitution : Cauchy (1815)| Autres symboles : |
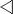 : inclus et
distingué (sous groupe)
»
Galois
: inclus et
distingué (sous groupe)
»
Galois

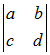 (déterminant) : Cauchy
(déterminant) : Cauchy

Cette page, comme toutes les autres, représente un travail personnel non négligeable de recherches. A ceux qui l'ont recopiée et publiée sur leur site sans pudeur ni scrupule (ou qui s'apprêteraient à commettre cette abomination...) , je recommande de vérifier les informations qu'elle contient car elles peuvent être entachées d'erreurs (y compris d'orthographe !) et de s'interroger sur les problèmes de déontologie, de bonne éducation et de droits d'auteur...
➔ Pour tout savoir, ou presque... :