ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 RECORDE Robert,
gallois, 1510-1558 |
Entre autres travaux algébriques portant principalement sur la résolution "par l'algèbre" de problèmes arithmétiques concrets usant de la méthode de fausse position ("The Grounde of Artes", Le Fondement de l'Art, 1542), on lui doit (The Whetstone of Witte, 1557) l'invention du signe d'égalité :
=
graphisme symbolisant l'idée de deux objets identiques ou jumeaux.
➔ Écrire a = b signifie que les objets notés a et b ne sont pas discernables. Il suit de cette acception que :
Ainsi x = 2 signifie que l'objet x n'est autre que le chiffre (nombre) 2. On dit que x égale 2 ou encore que x est égal à 2.
L'égalité
est parfois malmenée à l'école et au collège. On doit prendre garde à écrire de
part et d'autre du signe = des objets mathématiques de même nature. Dire les
segments sont égaux peut signifier que les segments en question ont la même
mesure mais ce n'est pas très rigoureux... il ne s'agira surtout pas d'écrire
[AB] = [CD]. A moins que A = c et B = D ! Par contre, une égalité vectorielle
comme :
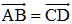
est tout à fait correct et n'implique nullement A = C et B = D. Il s'agit en fait d'une égalité de classe d'équivalence.
➔ Pour en savoir plus :
Clavius