ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Vecteur : flèche ou pas flèche...

Vers 1850, lorsque Hamilton définit le concept de vecteur, la notation surlignée fléchée :

pour désigner un vecteur n'est pas encore utilisée. On lui préférait les caractères gothiques ou (et encore aujourd'hui en imprimerie) les lettres grasses, souvent italiques : AB.

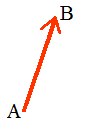Par contre le graphisme fléché (segment muni d'une flèche à son extrémité pour en indiquer le sens) remonte à fort longtemps puisqu'on le retrouve chez Stevin (fin du 16è siècle).

En France, la notation surlignée fléchée apparaît dans les années 1930 chez les physiciens et se propage lentement en mathématiques. Dans l'enseignement, elle coïncida longtemps avec la notation AB.

Cette notation initiée par Argand en 1806 dans le cadre de l'interprétation géométrique des nombres complexes, était encore utilisée en 1909 par Appell dans son Cours de mécanique et, encore trois décennies plus tard par A. Grevy, professeur au lycée Saint-Louis, dans son Traité de géométrie (1940) ! A cette même époque cependant, cette notation désigne, chez certains auteurs, la mesure algébrique du segment AB distincte de la notation vectorielle

Au tout début du 20è siècle, voici comment le Nouveau Larousse illustré (Dictionnaire Encyclopédique Universel, sous la direction de Claude Augé, 7 volumes) définit un vecteur :

• On appelle vecteur une droite AB ayant une direction, un sens et une grandeur (celle de la longueur AB, essentiellement positive). Les points A et B se nomment respectivement l'origine et l'extrémité du vecteur AB. Deux vecteurs sont égaux lorsqu'ils possèdent une direction, un sens et une grandeur identiques, quelles que soient du reste leurs positions dans l'espace. On n'altère donc pas un vecteur en le transportant parallèlement à lui-même; aussi, pour désigner un vecteur de position déterminée on se sert souvent du mot segment.

Il s'agit là du point de vue de Laisant qui, suite à Bellavitis, complétait sa Théorie des équipollences en 1887. De nos jours, étant revenu dans les collèges et les lycées à des définitions plus concrètes après les excès des mathématiques modernes, cette définition pourrait être adoptée à condition d'éviter la confusion entre vecteur, droite et segment...

25 ans plus tard, le Larousse du XXè siècle (6 volumes, sous la direction de Paul Augé) reprend l'article sous la forme :

• segment rectiligne que l'on suppose parcouru par un mobile allant d'une extrémité à l'autre. Le sens défini par le mobile qui se déplace sur le segment est le sens du vecteur, son point de départ est l'origine du vecteur, son point d'arrivée est l'extrémité. On désigne un vecteur par la notation AB, A étant l'origine et B l'extrémité du vecteur.

Toujours pas de flèche ! Et on peut regretter là le seul support mécanique. La formule de Chasles est également donnée en notant mes AB la mesure du segment orienté, ce que nous notons aujourd'hui AB.

On attribue généralement à Chasles et/ou Möbius la paternité du concept de vecteur en tant que segment orienté.
On oublie systématiquement les travaux de Wessel et d'Argand !

 ➔  Curieusement, Émile Borel éminent mathématicien français parle d'abscisse sur un axe en écrivant, dans son Algèbre et Géométrie du second degré (1946), x = OM/OA en expliquant qu'il faut considérer ce nombre comme le rapport de deux vecteurs OM et OA, OA désignant l'unité de longueur, le rapport étant positif ou négatif suivant que les vecteurs OM et OA ont même sens ou non.

Sans barre, ni flèche. Rien ! Mais il précise vecteur OA en adoptant la même notation pour l'unité de longueur. Plus tard encore, en 1952, dans L'imaginaire et le réel, Émile Borel parle de "vecteur OM" toujours sans surlignement d'aucune sorte.

On voit donc que notre notation fléchée d'aujourd'hui fut loin d'être un standard. Cependant, à partir de 1960, la notation surlignée fléchée semble adoptée définitivement. D'ailleurs, en 1955, Larousse publie son Encyclopédie méthodique où les notations actuelles sont déjà utilisées.

Ci-dessous, la rédaction relative à la formule de Chasles :

Dans la même encyclopédie Larousse, une étude des transformations usuelles (translation, rotation, homothétie, inversion) est rédigée avec précision en usant de notations tout à fait modernes, y compris celles des angles orientés de droites.

 ➔   La notation fléchée est claire et pratique en écriture manuscrite : elle distingue bien un vecteur de la longueur du segment [AB], notée AB, ou de la mesure algébrique d'un tel segment orienté, notée AB.

Cette notation est cependant très contraignante pour la  mise en page : il faut passer par un éditeur de formules mathématiques à chaque occurrence d'un vecteur, raison pour laquelle ChronoMath utilise souvent la notation "à l'américaine", le gras oblique : est alors noté AB.