
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges


» Quoique fils de peintre décorateur, on ne le confondra pas avec son illustre homonyme, le peintre Paolo Caliari Véronèse (1528-1588) à qui l'on doit, entre nombreux autres célèbres tableaux, Les noces de Cana (Musée du Louvre).
Né près de Venise, Véronèse y fait ses études secondaires et débute une formation d'ingénieur qu'il abandonnera pour trouver du travail, à Vienne (Autriche), dans l'aménagement hydraulique du Danube. Il reprendra des études de mécanique à l'Institut polytechnique de Zürich (1873) et se découvre un penchant pour les mathématiques pures, tout particulièrement en géométrie projective.
← Portrait et éléments de biographie extraits du site de Paola Cantu, avec son aimable autorisation.
En 1876, Véronèse se fait brillamment remarquer par Frobenius au cours d'un séminaire, ce qui lui vaudra, avec l'appui de Cremona, un poste d'assistant dans l'enseignement de la géométrie descriptive et projective à l'université de Rome (1877) puis à Leipzig où il rencontra Klein. Il succèdera à Bellavitis (1881) à l'université de Padoue (Padova) où il sera le professeur de Castelnuovo. Véronèse fut aussi député et sénateur.
Dans les années 1880, Véronèse développe une théorie de géométries euclidiennes abstraites à n dimensions (Grassmann avait auparavant abordé le sujet sur le plan vectoriel) et s'intéresse au problème de la continuité de la droite géométrique mise en correspondance avec la "droite" numérique (axe gradué) en construisant une géométrie non archimédienne (1889), c'est à dire refusant l'axiome d'Archimède.
Les nombres réels ont été récemment construits (on est à l'époque de Hilbert, Dedekind et Cantor) et la communauté mathématique de l'époque, Peano en particulier, estimant l'axiome incontournable, vit dans cette géométrie un certain manque de rigueur. Dehn montra d'ailleurs que l'axiome d'Archimède était nécessaire en dimension 3. Cependant, tout comme l'analyse non standard et les géométries non euclidiennes, cette construction apportera plus tard une pierre supplémentaire à la théorie des modèles.
Quoi qu'il en soit, l'œuvre magistrale de Véronèse portera sur les fondements de la géométrie (1891) où il introduit, à l'instar de Klein, la théorie des groupes. Après les travaux amorcés par Chasles, il est considéré, avec son compatriote Corrado Segre (1863-1924) comme l'initiateur de la géométrie algébrique que développeront, en particulier, Castelnuovo et Enriques, ses compatriotes, Max Noether en Allemagne et Zariski aux États-Unis.
» Max Noether , Lefschetz , Langlands , Zariski , Hodge , Kodaira , Voisin, ...
|
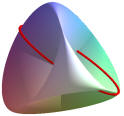
Surface de Véronèse : |
A tout point du plan projectif, de coordonnées homogènes (x, y, z) on associe canoniquement (par plongement) le point de coordonnées (x2, y2, z2, xy, xz, yz) de l'espace projectif de dimension 5. La surface de Véronèse est alors l'hypersurface, image de la "sphère" x2 + y2 + z2 = 1 du plan projectif.
Source
image :
Université Technique de Vienne
Cette surface abstraite n'est pas représentable ! Mais son volume est 2π2. Les projections d'une surface de Véronèse sur l'espace projectif 3D sont des surfaces de Steiner étudiées auparavant par ce mathématicien suisse en 1844.
La notion générale de surface : »
➔ Pour en savoir plus :