ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

AITKEN Alexander Craig, néo-zélandais, 1895-1967

 !  On ne confondra Alexander Craig Aitken avec l'astronome américain Robert Grant Aitken (1864-1951) qui décrivit le comportement des étoiles doubles. Source portrait et éléments biographiques : université d'Otago.

Aitken entreprend des études dans sa ville natale de Dunedin (Nouvelle-Zélande, île du Sud, dite de Jade) à l'université d'Otago. Mais la première guerre mondiale l'oblige à s'enrôler sous les drapeaux anglais et il participa, en France, à la célèbre bataille de la Somme où il sera grièvement blessé.

 i  La Nouvelle Zélande fut découverte par les Hollandais au 17è siècle (A.J. Tasman, 1642, qui donna son nom à la mer de Tasman et à la Tasmanie). Elle se compose de deux îles principales : l'île du Nord (île Fumante) et l'île du Sud (île de Jade). Plus d'un siècle plus tard (1769), le célèbre navigateur anglais James Cook s'en empara au profit de la Grande-Bretagne. Puis vinrent les Français avec Surville mais les Anglais réussirent à signer un traité avec les tribus Maoris (1840). La Nouvelle-Zélande devient colonie britannique; elle est gouvernée depuis l'Australie. Indépendante en 1931, elle est encore membre du Commonwealth.

Après la guerre, Aitken reprend ses études et obtient un poste au lycée de garçons d'Otago. En 1923, grâce à une bourse d'études, il achève ses études en mathématiques économiques à Édimbourg (Edinburgh, Écosse) tout en s'intéressant à l'analyse numérique et à la théorie des matrices. Maître de conférence, puis professeur, Aitken enseigna les mathématiques économiques et la statistique à l'université d'Édimbourg jusqu'à sa retraite en 1965. Il publia, en particulier, Statistical mathematics (1945). Il fut élu membre de la Royal Society en 1936.

Prodigieux calculateur, il s'intéressa, à l'instar de Ramanujan, à des méthodes d'accélération de convergence dans des algorithmes itératifs (suites et séries, résolution d'équations et de systèmes d'équations) qui inspirèrent les mathématiciens contemporains dans la mise en œuvre d'algorithmes numériques traités par ordinateur.

Méthode du Δ2 (accélération de convergence) :

Complétant des travaux de Daniel Bernoulli sur la résolution approchée des équations algébriques au moyen de suites récurrentes (On Bernoulli's Numerical Solution of Algebric Equations, Édimbourg-1926), Aitken construit, à partir d'une suite convergente (xn) du type xn+1 = f(xn), une suite (yn) convergeant "plus vite" vers la même limite :

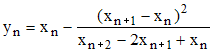
soit, en posant Δxn = xn+1 - xn    et  Δ2xn = Δxn+1 - Δxn :

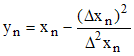
d'où l'appellation de la méthode.

La suite (yn) converge "plus vite" que (xn) vers le réel α si le rapport | yn - α | / | xn - α | a pour limite 0. On parle de l'ordre d'un algorithme : en posant εn = | xn - α |, l'algorithme sera d'ordre p si εn+1 = O(εnp).

 Théorème du point fixe pour les suites du type xn+1 = f(xn) : »       » Notations de Landau

∗∗∗ 
Preuve de l'accélération de convergence

La fonction f est supposée dérivable sur l'intervalle d'étude J contenant le point α, point fixe de f et limite de la suite (xn). On suppose en outre que sur J, Max|f '(x)| = K < 1. On pose alors εn = xn - α.
a) Montrer que la suite de terme général un = εn+1/εn converge vers L = f '(α).
b) Exprimer le rapport (yn - α) / (xn - α) en fonction de un et un+1. En déduire que ce rapport tend vers 0.

Il faut cependant noter que pour n grand, la convergence de la suite (xn) implique que xn+2 , xn+1 et xn sont très voisins, ce qui impliquera d'importantes erreurs de calcul "machine".

Pour cette raison, il est préférable d'écrire une formule "plus stable" : une petite manipulation de la formule définissant yn conduit à :

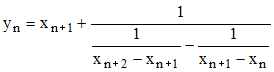
Calcul de ln2 et accélération de convergence : »               Formule de Machin : »

 ➔   Pour en savoir plus :

Julia  Ackermann
© Serge Mehl - www.chronomath.com