Ln2 selon Mercator

ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Calcul de ln 2 au moyen de la série harmonique alternée
» accélération de convergence

L'objectif est ici d'accélérer la convergence s'une série convergente afin de trouver une bonne valeur approchée de sa somme. Cette simple et très efficace accélération de convergence est empruntée au mathématicien russe Vladimir Ivanovich Smirnov (1887-1974), dans son cours de mathématiques supérieures, Tome 1, ch. IV, Traduction française : Éd. Mir, Moscou - 1981.

Dans son Logarithmotechnia, Nicolaus Mercator calcule l'aire sous l'hyperbole x → 1/x en exhibant le développement :

x - x²/2 + x³/3 - x⁴/4 + x⁵/5 - ... (série de Mercator)

correspondant au développement en série de la fonction x → ln(1 + x) pour |x| ≤1, ln désignant le logarithme népérien.

Cette série est convergente et lorsque x = 1, elle est appelée série harmonique alternée, eu égard à la série harmonique (laquelle est divergente) : la somme 1 +1/2 + 1/3 + 1/n + ... est infinie.

Ici, selon un résultat de Leibniz, cette série étant alternée, l'erreur faite en limitant la somme au rang n est inférieure au terme de rang n + 1, donc inférieure à 1/n :

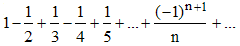
On conçoit donc que la convergence sera lente.

Programmation JavaScript de la méthode :

Les résultats sont conformes à la théorie : la convergence en 1/n est très lente.

Rappel : ln 2 = 0,6931471805599...

n = 1000 : ln 2 = 0,6926.
L'erreur est inférieure à 1/1000
n = 10000 : ln 2 = 0,6931...
L'erreur est inférieure à 1/10000

<SCRIPT LANGUAGE=JavaScript>
function go()
{
n=0
ln2=0
sgn=-1
while (1)
{
n++
sgn=-sgn
ln2=ln2+sgn/n
if (n%100==0)
{
if(!confirm("n="+n+" Ln2 = "+ln2)) return}
}
}
</SCRIPT>

@ Visualisation des calculs au moyen du tableur

Accélération de la convergence :

On peut accélérer la convergence par un changement de variable : changeons x en -x dans la série de Mercator. On obtient alors par différence :

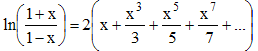
changeons maintenant x en :

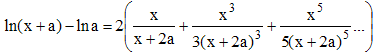
La convergence sera d'autant plus rapide que x est petit devant a.

Pour calculer ln 2, on choisit x = 1 et, successivement a = 15, a = 24 et a = 8; notons respectivement s₁, s₂ et s₃ les sommes entre crochets obtenues pour ces valeurs.

On a :

4Ln 2 - Ln 3 - Ln 5 = 2s₁

2Ln 5 - Ln 3 - 3Ln 2 = 2s₃

2Ln 3 - 3Ln 2 = 2s₂

Et par combinaison, on obtient :

ln 2 = 8s₁ + 6s₂ + 4s₃

Programmation JavaScript de la méthode d'accélération :

Rappel : ln 2 = 0,6931471805599...

n = 1, ln 2 = 0,6926...
n = 3, ln 2 = 0,69314...
n = 5, ln 2 = 0,69314718...
n = 7, ln 2 = 0,693147 4718055...
n = 9, ln 2 = 0,6931471805599...
n = 11, ln 2 = 0,6931471805599454 (stationnaire)

Pas mal, voire impressionnant...

! La 16è décimale n'est pas assurée car on est là en limite des possibilités du langage (16 chiffres significatifs). On peut améliorer les calculs en usant d'artifices comme ici ou là...

<SCRIPT LANGUAGE=JavaScript>
function go2()
{
n=1;
s1=1/31;s2=1/17;s3=1/49;
k1=s1;k2=s2;k3=s3;
ln2=8*s1+6*s2+4*s3;
if(!confirm("n="+n+" Ln2 = "+ln2)) return
while (1)
{
n=n+2;
k1=k1/31/31;
k2=k2/17/17;
k3=k3/49/49;
s1=s1+k1/n;
s2=s2+k2/n;
s3=s3+k3/n;
ln2=8*s1+6*s2+4*s3;
if(!confirm("n="+n+" Ln2 = "+ln2)) return}
}
</SCRIPT>

Un calcul aléatoire de ln2 : » La méthode d'accélération, dite Δ² d'Aitken : »