ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Cas d'égalité et somme des angles des triangles     niveau 2nde     » #2 , #3

Observe bien cette figure géométrique :

• Le triangle ABC est isocèle de sommet principal A avec AB > BC.

• Le côté [BC] est prolongé en [BE] et le côté [AB] en BD de sorte que BD = CE = AB - BC.

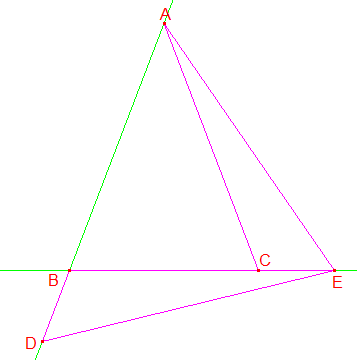
1°/ Comparer les triangles ACE et EBD.

2°/ Justifier que le triangle ABE est isocèle.

3°/ Justifier que le triangle EAD est isocèle.

4°/ Montrer que l'angle ^ADE est égal à la demi-somme des angles ^BAC et ^AED.

1°/ Par construction, on a BD = CE. Le côté [BE] du triangle EBD mesure BC + AB - BC =AB. Le côté [AC] du triangle ACE mesure AB puisque ABC est isocèle de sommet principal A.

L'angle ^ACE du triangle ACE mesure 180° - ^ACB. L'angle EBD du triangle EBD mesure 180° - ^ABC. Or ^ABC = ^ACB.

En conclusion, les triangles ACE et EBD ont un angle égal compris entre deux côtés de même mesure : ils sont donc égaux (superposables) en vertu du second cas d'égalité des triangles.

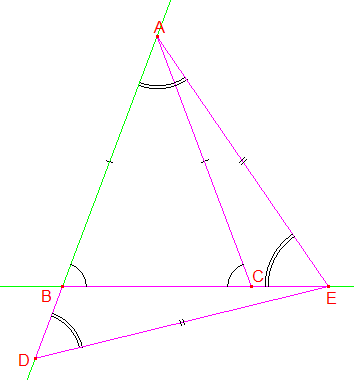
2°/ Par construction, on a AB = BE, donc ABE est isocèle de sommet principal B.

3°/ Les triangles ACE et EBD étant égaux, au plus grand angle (^EBD = ^ACE) est opposé le plus grand côté. C'est ainsi que les côtés [ED] et  [EA] sont homologues : on a ED = EA, c'est dire que le triangle EAD est isocèle de sommet principal E.

4°/ D'après 2°/, on ^BAE = ^AEB et selon 3°/, ^ADE = ^DAE = ^AEB.

Par suite, 2 ^ADE = ^DAE + ^AEB = ^BAC + ^CAE + ^AEB = ^BAC + (^DEB + ^AEB).

Donc 2 ^ADE = ^BAC + ^AED, autrement dit : ^ADE = (^BAC + ^AED)/2.