
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
» Notion générale d'enveloppe , Recherche de l'équation de l'enveloppe | Approche similaire | Cas d'une famille d'ellipses |
Dans un repère orthonormé (Ox,Oy), on considère deux points mobiles A et B respectivement placés sur [0x) et [0y).
L'objectif est d'étudier l'enveloppe des droites (AB) lorsque le segment [AB] glisse sur les axes, la distance AB restant constante. On choisit ici AB = 10.
➔ Concrètement, on pourra obtenir l'enveloppe des droites (AB) au moyen d'une réglette en carton de 10 cm de long que l'on fera glisser le long de (Ox) et (Oy) de sorte qu'une de ses extrémités soit sur (Oy) et l'autre sur (Ox); on trace à chaque fois le segment [AB] correspondant.
On peut aussi planter des petits clous sur une planchette, répartis sur les axes Ox et Oy de sorte que la distance entre un clou de Ox corresponde à un clou de Oy espacés de 10 cm.
Passons maintenant à l'aspect théorique :
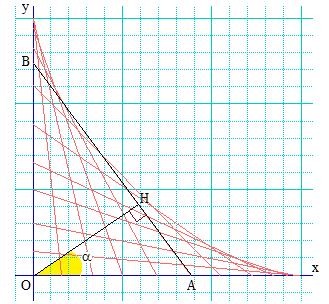
On note H le projeté orthogonal de O sur [AB[ et lorsque H est distinct de l'origine O, α désigne une mesure de l'angle de droites ^(Ox,OH). On se propose de déterminer et de construire l'enveloppe (E) des droites (AB) lorsque α décrit [0,π/2].
♦ 1. Montrer qu'une équation cartésienne de la droite (AB) est :
♦ 2. Par dérivation (cf. théorie), et résolution du système homogène en x et y, montrer qu'une équation paramétrique de (E) est donnée par :
x = 10.sin3α
y = 10.cos3α
La courbe s'étudie facilement et par des considérations de parité et de symétrie, on peut prolonger l'étude à [0,2π] et obtenir l'astroïde en entier.
♦ 3. En utilisant que sin2α + cos2α = 1, montrer qu'une équation cartésienne de l'astroïde est dans notre cas :
Plus généralement l'astroïde a donc pour équation cartésienne :
x2/3 + y2/3 = a
Famille des droites x.cos α + y.sin α - 5sin 2α = 0, décrivant [-π,+π] par pas de 0,05 :
∗∗∗
Astroïde en tant qu'enveloppe d'une
famille d'ellipses :
On connait bien l'ellipse définie par son
équation cartésienne de la forme x2/a2 + y2/b2
= 1 avec a et b strictement positifs. Soit k > 0. Fixons a + b = k.
Montrer que
lorsque a et b varient sous cette contrainte, l'enveloppe de la famille
d'ellipses est une astroïde :
Si vous séchez après avoir bien cherché : ››››
•••
»
Astroïde
et développée de
l'ellipse | Néphroïde et enveloppe
d'une famille de cercles |
Parallèles d'une courbe