ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
» Notion générale d'enveloppe | Recherche de l'équation de l'enveloppe | » Astroïde en tant que famille de droites |
Dans un repère orthonormé (Ox,Oy), on connait bien l'ellipse définie par son équation cartésienne de la forme :
x2/a2 + y2/b2 = 1 avec a et b strictement positifs.
Soit k > 0. Fixons a + b = k. Montrer que lorsque a et b varient sous cette contrainte, l'enveloppe de la famille d'ellipses est une astroïde.
Si vous séchez après avoir bien cherché : ››››
» Néphroïde et enveloppe d'une famille de cercles
| Solution : |
a + b étant fixé à la valeur k, on a b = k - a et b > 0 impose a < k, donc 0 < a < k. L'équation de notre famille d'ellipses paramétrée par a s'écrit :
x2/a2 + y2/(k - a)2 - 1 = 0, a > 0
Selon la théorie, en posant f(x,y,a) = x2/a2 + y2/(k - a)2 - 1, nous recherchons une équation paramétrique sous la forme :
x = u(a)
y = v(a)
sous les conditions : f(x,y,a) = 0 et f '/a(x,y,a) = 0.
(1/a2)' = -2/a3 et [1/(k - a)2]' = 2/(k - a)3. Nous sommes amenés à résoudre le système :
x2/a2 + y2/(k - a)2 = 1
- x2/a3 + y2/(k - a)3 = 0
Posons X = x2, Y = y2 :
X/a2 + Y/(k - a)2 = 1
- X/a3 + Y/(k - a)3 = 0
Le déterminant D de ce système se calcule facilement :
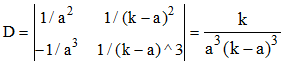
On en déduit, sous la condition 0 < a < k :
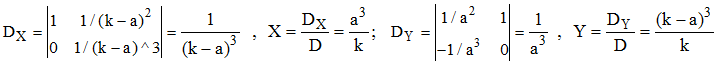
On revient à x et y : kx2 = a3 et ky2 = (k - a)3. On prend les racines cubiques : k1/3x2/3 = a et k1/3y2/3 = k - a. En sommant, on en déduit :
x2/3 + y2/3
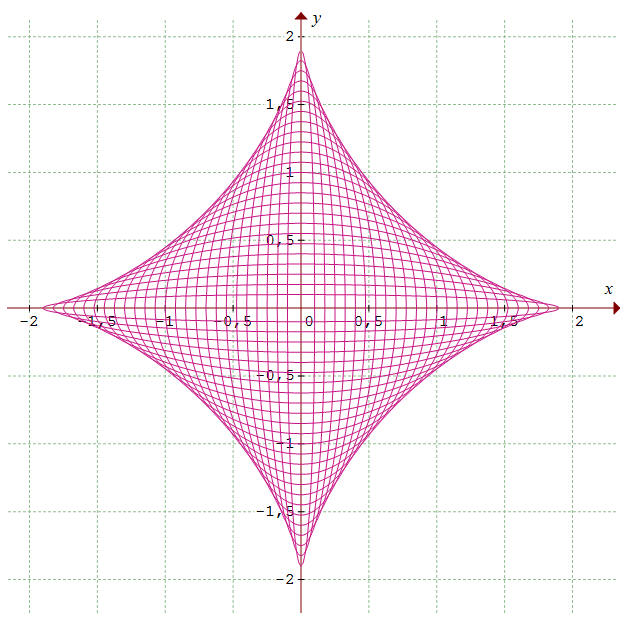
= k / k1/3 = k2/3Il s'agit bien de l'équation cartésienne de l'astroïde de centre l'origine. Ci-dessous, l'enveloppe obtenue par Graphmatica lorsque k = 2, a décrivant l'intervalle ]0,2[ par pas de 0,05.
➔
Un pas plus petit permettrait de '' s'approcher " plus des bornes ± 2 mais un trop grand nombre d'ellipses nuirait à la lecture du graphique.