astroïde #2

ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

L'astroïde en tant qu'enveloppe d'une famille de droites
Thème semblable proposé en exercice | Astroide en tant qu'enveloppe d'une famille d'ellipses

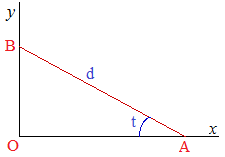
L'astroïde (étymologiquement : "qui ressemble à un astre", "en forme d'étoile") est une hypocycloïde. On peut aussi la générer de la façon suivante : considérons un repère orthonormé (Ox,Oy).

L'extrémité A d'une "baguette" [AB] de longueur d glisse sur [Ox), B reposant sur [Oy). L'enveloppe de cette famille de segments est un "quart" d'astroïde.

En effet, posons t = ^OAB. Les coordonnées de A et B sont simples à évaluer : A(dcos t;0) et B(0;dsin t).

L'équation générale des segments peut s'écrire :

d'où :

x.sin t + y.cos t = d.sin t.cos t , avec o < t < π/2 (1)

Si votre navigateur accepte les applets Java (» extension CheerpJ) :
Manuellement, la courbe sera obtenue en déplaçant le point P.
L'astroïde est obtenue entièrement par le programme au moyen de symétries par rapport aux axes.
Vous pouvez aussi agrandir/diminuer en déplaçant le point bleu de la "baguette"

➔ Si votre navigateur ne prend pas en charge les Applets Java de Cabri-géomètre, voici ce que vous devriez obtenir au fur et à mesure du déplacement de P :

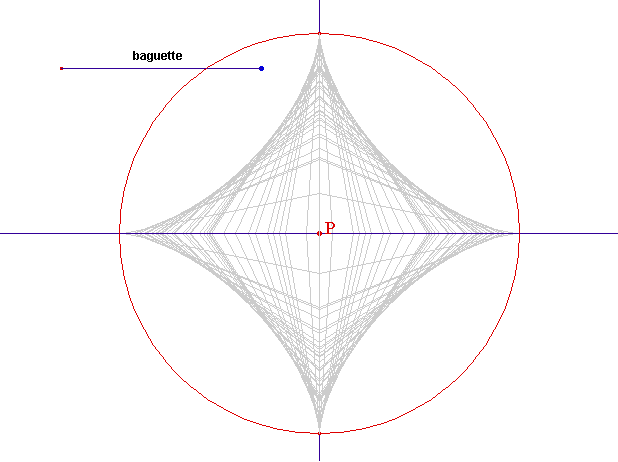
Selon la théorie, l'équation de l'enveloppe est obtenue en dérivant (1) par rapport à t. Le système obtenu fournit facilement une équation paramétrique de la courbe :

x = d.cos³t , y = d.sin³t

Prenons la racine cubique, puis élevons au carré (licite puisque tout est positif !). En coordonnées cartésiennes, l'équation s'écrit donc, puisque cos²t + sin²t = 1 :

x^2/3 + y^2/3 = d^2/3

➔ Remarquer que l'équation trouvée x = d.cos³t , y = d.sin³t est compatible avec l'équation des trochoïdes de la forme :

x = k(3cos t + cos 3t) , y = k(3sin t - sin 3t)

car, par application de la formule de Moivre ou simple calcul de cos3t = cos(2t + t) et sin3t = sin(2t + t), on a :

cos³t = (3cos t + cos 3t)/4 et sin³t = (3sin t - sin 3t)/4

→ ci-dessus : mosaïques du palais des empereurs byzantins , musée d'Istanbul. Ce ne sont pas des astroïdes au sens mathématique : vous pouvez voir soit des rosaces à 4 branches (quarts de cercles) soit des "astroïdoïdes" (qui ressemblent à des astroïdes...) formés par des quarts de cercles (vus concaves) et agrémentées d'un carré central.

» Astroïde et développée de l'ellipse | Quadrifolium (en tant que podaire de l'astroïde)