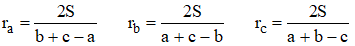ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Application des angles inscrits : la formule des sinus    TD 3ème/1ère

Voici une application simple de la notion d'angle inscrit dans un cercle, étudiée dès la classe de 3ème mais dont l'usage est très peu usité, voire occulté.

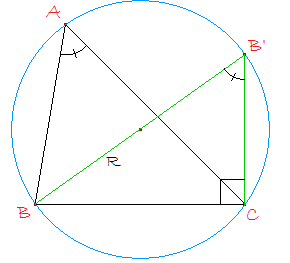
Niveau 3ème/2nde : on considère la figure ci-dessus. On note R le rayon du cercle circonscrit au triangle ABC. Soit B' le point diamétralement opposé à  B. Justifier que ^BAC = ^BB'C. En déduire l'égalité : 

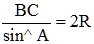
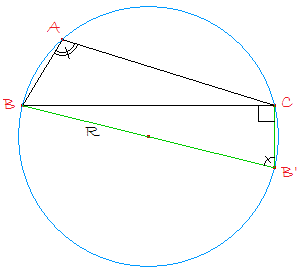
Niveau 2nde : En considérant la figure ci-dessous, vérifier que le résultat ci-dessus est encore valable lorsque le triangle ABC possède un angle obtus. On utilisera la formule sin x = sin(180° - x) ou, en radians : sin x = sin(π - x).

On note a = BC, b = AC et c = AB. Justifier aolors la célèbre formule des sinus (ou règle des sinus) dans le triangle plan, parfois attribuée à Al-Kashi mais qu'Al-Biruni avait utilisée et prouvée près de quatre siècles auparavant :

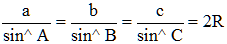
Cette formule, associée si nécessaire à la formule d'Al-Kashi :

a² = b² + c² - 2bc.cosÂ

permet de "résoudre" des triangles, c'est à dire calculer les angles et les côtés d'un triangle lorsque l'on connaît au moins trois éléments :

1. Trois côtés : formule d'Al-Kashi pour le calcul de deux angles puis ^A + ^B + ^C = 180°.

2. Deux ou trois angles : indétermination des côtés; on prend par exemple BC = a comme unité et on calcule AB et AC en fonction de a au moyen de la formule des sinus.

3. Deux côtés et un angle : si  les côtés connus sont ceux de l'angle connu, on calcule le côté manquant au moyen de la formule d'Al-Kashi et on se ramène au cas 1. Sinon, la formule des sinus permet de calculer le sinus d'un second angle. Le problème sera insoluble si ce dernier est supérieur à 1. On peut également ramener le problème à une équation du second degré au moyen de la formule d'Al-Kashi : on peut avoir 0, 1 ou 2 solution(s).

4. Un  côté et 2 angles : on obtient le troisième angle comme supplément à 180° et on se ramène au cas 1 sans indétermination puisque l'on connait un côté.

Programme JavaScript de résolution de triangles : »

∗∗∗ 
Deux cas élémentaires de résolution de triangles  | Autres cas de résolution de triangles (4 exercices)

 ➔  La connaissance de l'aire S d'un triangle fournit des formules intéressantes : de la formule ½bc × sin^A, on déduit :  abc = 4R × S, relation que l'on peut retenir sous ces deux autres formes :

Dans un triangle de côtés a, b et c, d'aire S et R désignant le rayon de son cercle circonscrit, on a :

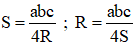
• Le rayon r du cercle inscrit fournit également une jolie formule :

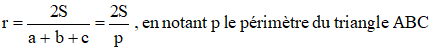
• Tout autant que les rayons des cercles exinscrits :