
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
TD niveau 3ème » Cas des cercles exinscrits | Cas du cercle circonscrit |
![]() Les exercices I et II sont indépendants. Le premier, qui
est plutôt un résultat de cours, montre une relation remarquable entre le rayon
du cercle inscrit dans un triangle, son périmètre et son aire. Le cas du cercle
circonscrit est traité ici...
Les exercices I et II sont indépendants. Le premier, qui
est plutôt un résultat de cours, montre une relation remarquable entre le rayon
du cercle inscrit dans un triangle, son périmètre et son aire. Le cas du cercle
circonscrit est traité ici...
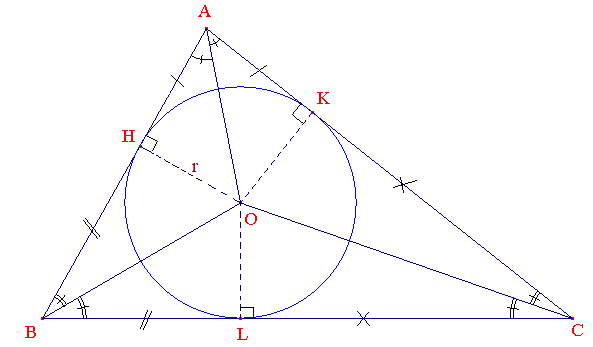
I - On considère un triangle ABC et son cercle inscrit de centre O, point de concours des bissectrices. Ce cercle est tangent intérieurement aux côtés du triangle. Son rayon est [OH], perpendiculaire à [AB] (» tangente à un cercle). On le retrouve en [OK], perpendiculaire à [AC] et en [OL], perpendiculaire à [BC]. On pose OH = r, BC = a, AC = b et AB = c
1°/ Calculer l'aire S du triangle ABC en fonction de r, a, b et c. En déduire :
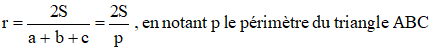
2°/ Justifier que si le triangle ABC est rectangle en A, on a :
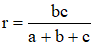
3°/ Justifier que si le triangle ABC est équilatéral de côté a, le rayon est :
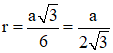
Cas du cercle circonscrit : » Cas des cercles exinscrits : »
II - On considère un triangle ABC dont le rayon du cercle inscrit, de centre O, est 3 unités. La projection orthogonale de O sur [AC] détermine AK = 3,5 et KC = 8,6. On demande de calculer AB et BC en arrondissant les valeurs trouvées à 0,1 près.
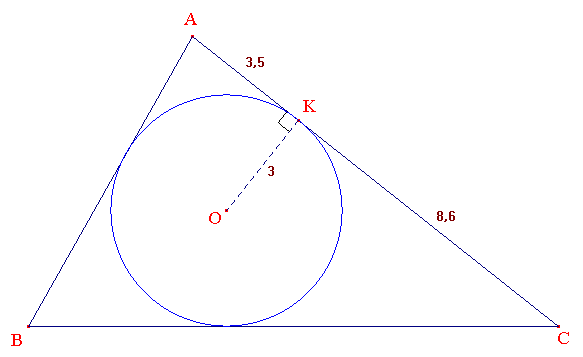
Indications :
En complétant judicieusement la figure, on calculera tout d'abord les mesures des angles ^A et ^C du triangle en arrondissant ces mesures au degré près. On en déduira la mesure de l'angle ^B.
Si vous séchez après avoir
bien cherché : ››››
| Solution : |

I - 1°/ Considérons les trois triangles BOC, AOC, AOB et . Leurs aires respectives sont ½r × BC, ½r × AC et ½r × AB. On a donc :
S = ½r × (BC + AC + AB), soit 2S = r × (a + b + c), d'où le résultat escompté :
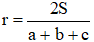
2°/ Trop facile...
3°/ Facile connaissant la hauteur h du triangle équilatéral de côté a :
h = a × sin(60°) = a√3/2.
II - Complétons la figure en codant et notant les mesures connues en utilisant un résultat important : les segments tangents issus d'un point extérieur à un cercle ont même mesure : AK = AH, BH = BL, CK = CL.
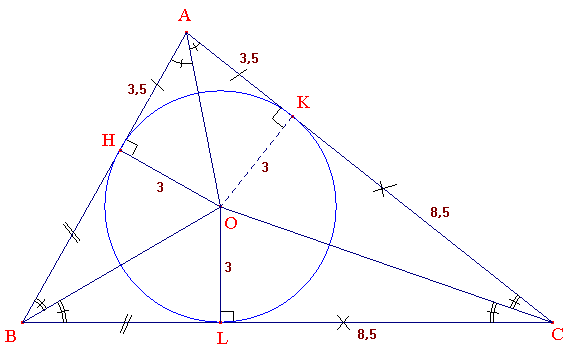
On note respectivement ^A, ^B et ^C les angles ^BAC, ^ABC et ^ACB. Dans les triangles rectangles AOK et COK, on a respectivement tan(^A/2) = OK/AK = 3/3,5 et tan(^C/2) = OK/CK = 3/8,5. La calculatrice fournit alors ^A/2 = 40.6..., soit ^A = 81° (arrondi au degré près) et ^C/2 = 19,4..., soit ^C = 39° (au degré près). On en déduit ^B = 180° - ^A - ^B = 60°.
Dans le triangle BOH, rectangle en H, on a OH = BH × tan(^B/2), d'où BH = BL = 3/tan 30° ≅ 5,2 cm.
En conclusion :
AB = 8,7 cm, BC = 13, 7 cm, AC = 12 cm.