ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Résolution de triangles     niveau 2nde/1ère       @ Utiliser le programme JavaScript
      » Al-Kashi et cas élémentaires | Autres cas | @ Conversion degrés décimaux/degrés sexagésimaux

 ➔   « Résoudre un triangle », c'est calculer la mesure de ses côtés et de ses angles au moyen de données le concernant : côté(s), angle(s), médiane(s), hauteur(s), rayon du cercle inscrit (ou circonscrit), etc. Dans le cas général, 3 données indépendantes sont nécessaires. Une exception simple est le triangle équilatéral (1 donnée : la mesure commune des côtés). Le triangle isocèle et le triangle rectangle sont également des cas particuliers se réduisant à deux données.

On se donne un triangle ABC de côtés BC = a, CA = b, c = AB, Les mesures de ses angles sont notées ^a, ^b, ^c. L'étude ci-dessous se limite à la résolution d'un triangle au moyen de données sur ses angles et ses côtés.

  (fig.1)

 Rappelons deux formules fondamentales :

Quatre cas fondamentaux se présentent :

  1. Trois côtés :
    On utilise la formule d'Al-Kashi ci-dessus pour le calcul de deux angles puis     ^a + ^b + ^c = 180°.

  2. Deux côtés et un angle :
    Si  les côtés connus sont ceux de l'angle connu, on calcule le côté manquant au moyen de la formule (r1) et on se ramène au cas 1. Sinon, la     formule des sinus permet de calculer le sinus d'un second angle. Le problème sera insoluble si ce dernier est supérieur à 1 ! On peut également ramener le problème à une équation du second degré au moyen de la formule (r1) : on peut avoir 0, 1 ou 2 solution(s).

  3. Un  côté et 2 angles :
    On obtient le troisième angle comme supplément à 180°; les côtés manquants sont calculés par la formule (r2) ci-dessus.
  4. Deux (donc trois) angles : il y a une infinité de solutions homothétiques (triangles semblables). Le côté a = BC sera pris comme unité : on est ramené au cas précédent.
Cas 1 : les trois côtés sont connus, on calcule les mesures de ^a, ^b et ^c en degrés décimaux :

Les côtés a, b et c sont connus. On peut calculer chaque angle au moyen de la formule d'Al-Kashi (r1). Le programme calculera ainsi cos^a et cos^b au moyen des formules :

Les mesures ^a et ^b seront obtenues au moyen de la fonction réciproque du cosinus, Arc cosinus, notée acos en JavaScript et cos-1 sur les calculatrices, qui nous fournira un angle compris entre 0° et 180° :

x = cos α ⇔ α = acos(x) , 0 ≤ α ≤ 180

La mesure ^c sera obtenue par ^c = 180 - ^a - ^b.

Discussion :   

L'inégalité triangulaire nous interdit de construire un triangle avec des données fantaisistes a, b et c. Nous devons honorer la double inégalité :

 |b - c | < a < |b + c|    (it)

La mesure de l'angle A est comprise au sens strict entre 0° et 180°. Dans cette plage de variation cos^a décroît de 1 à - 1. Sous la condition cos^a = (b2 + c2 - a2)/2/b/c, montrons que - 1 < cos^a < 1 équivaut à (it) :

- 1 < cos^a < 1 ⇔ -2bc < -2bc × cos^a < 2bc ⇔ b2 + c2 - 2bc < a2 < b2 + c2 + 2bc ⇔ (b - c)2 < a2 < (b + c)2  ⇔ (it)

Afin de valider la construction, le programme se contentera donc d'un test sur la valeur calculée de cos^a en fonction de a, b et c.

Cas 2.1 : on connaît un angle et ses 2 côtés, par exemple ^BAC, et les cotés b = AC et c = AB :

Cas élémentaire : unique solution comme le montre la figure ci-dessous où l'on trace un angle ^xAy , suivi de la construction de B tel que AB = c et C tel que AC = b :

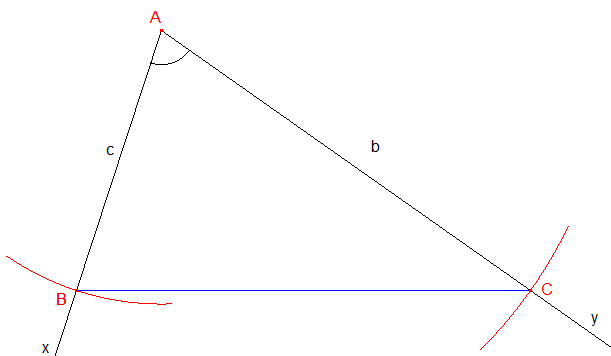
En calculant a = BC au moyen de la formule (r1), on se ramène au cas précédent.

Cas 2.2 : on connaît un angle, un de ses côtés et le côté opposé, par exemple ^BAC, et les cotés b = AC et a = BC :

Ce cas est plus délicat. Le "souci" porte sur l'existence et l'unicité du sommet B suivant que l'angle A est trop ouvert (angle obtus) et/ou a = BC trop petit par rapport à b = AC. Dans le cas ci-dessous il n'y a pas de solution :

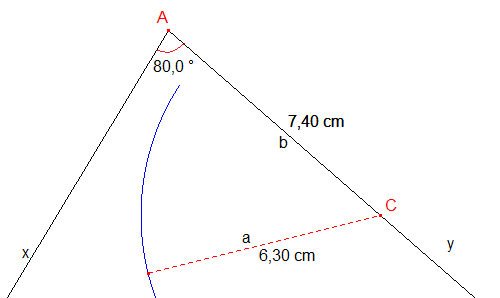
Discussion :   

La formule des sinus (r2), à savoir a/sin^a = b/sin^b = c/sin^c va ici nous être utile. Tout d'abord une condition nécessaire apparaît sur la valeur calculée du sinus de l'angle B. On a bien sûr sin^b > 0 car sin^a, sinus d'un angle compris entre 0° et 180°, est positif, mais il n'est pas assuré d'avoir :

sin^b = b/a × sin^a ≤ 1

Dans le cas présenté ci-dessus, cette condition n'est pas remplie.

 ➔   Le cas sin^b = 1 correspond à un triangle rectangle en B. 

♦  Si a > b, le cercle de centre C de rayon a coupe [Ay) en un unique point B. C'est dire que la condition sur sin^b est remplie. On calcule sin^b. La fonction réciproque du sinus, Arc sinus, notée asin en JavaScript et sin-1 sur les calculatrices, nous fournira un angle α compris entre 0° et 90° (car sin^b > 0) :

x = sin α > 0 ⇔  α = asin(x) , 0 ≤ α ≤ 90°

Ce qui fournira ^b puis ^c = 180° - ^a - ^b. On aura enfin c = a × sin^c/sin^a.

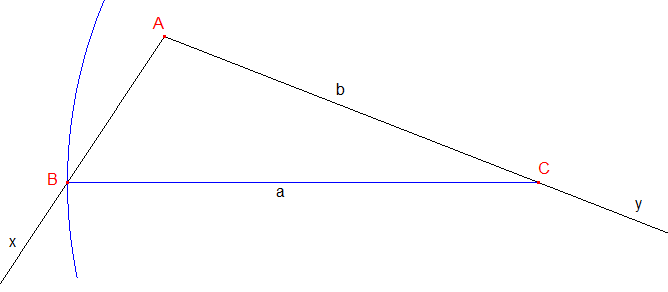
ci-dessus : Angle ^A obtus, a > b, solution unique

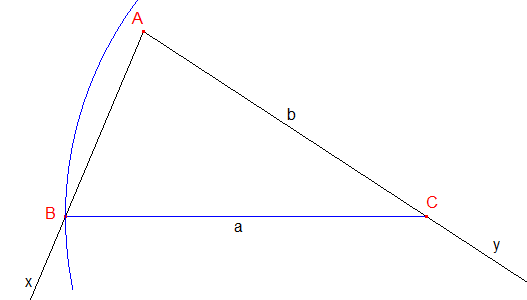
ci-dessus :  Angle ^A aigu, a > b, solution unique

♦  Si a = b, pas de solution si A est obtus ou droit. Solution unique si A aigu : triangle isocèle de sommet principal C.

♦  Si a < b et l'angle A obtus, le cercle de centre C de rayon A ne coupe pas la demi-droite [Ax) : pas de solution.

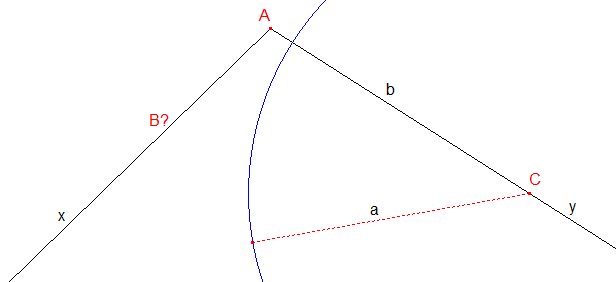
ci-dessus :  Angle ^A obtus, a < b, pas de solution

♦  Si a < b et l'angle A aigu, il y a 0, 1 ou 2 solutions que l'on pourra visualiser au moyen de la figure dynamique Cabri-géomètre si votre navigateur le permet. Eu égard aux données, la formule (r1) fournit :

c2 - 2bc × cos^a + b2 - a2

Cette équation du second degré fournit un discriminant réduit Δ' = a2 - b2sin2^a et la formule des sinus a/sin^a = b/sin^b élevée au carré permet d'écrire b2sin2^a = b2sin2^b, puis Δ' = a2 cos2^b et enfin :

c = b × cos^a ± a × cos^b

Sans oublier la condition sur l'angle B : b/a × sin^a = sin^b ≤ 1. Concluons :

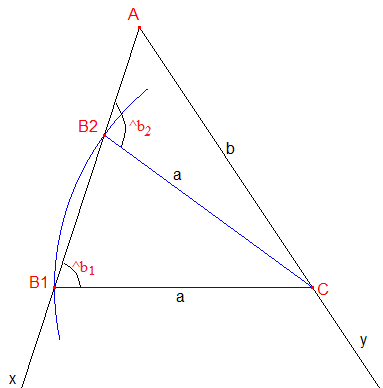
ci-dessus :  ^BAC aigu, deux solutions


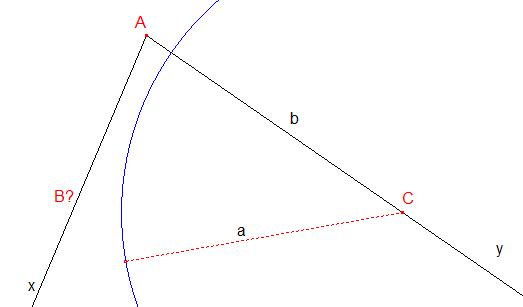
ci-dessus :  ^BAC aigu, pas de solution car b/a × sin^a > 1

Cas 3 : on connaît un côté et deux angles, par exemple a = BC et ^b et ^c :

On calcule le troisième angle, ici ^a = 180° - ^b - ^c. Les côtés b = AC et c = AB seront ensuite calculés au moyen de la formule des sinus (r2).

Exemple : ^a = 105°, ^b = 45°. La somme des angles égalant 180°, on a ^c = 30°. Si a =1, la formule des sinus s'écrit 1/sin105° = b/sin45° = c/sin30°. D'où b = sin45°/sin105° ≅ 0,732; c = sin30°/sin105° ≅ 0,518. Si la mesure de a est 23 m, alors b = AC = 23 × 0,732 ≅ 16,84 m, c = AB = 23 × 0,518 ≅ 11,91 m.

Cas 4 : on ne connaît que les angles :

Connaissant deux (donc trois) angles, il y a une infinité de solutions homothétiques (triangles semblables). En choisissant BC comme unité de mesure, soit a = 1, on est ramené au cas 3 ci-dessus. Dans la pratique, une fois connue ou décidée la mesure de a = BC, les valeurs calculées de b et c devront être multipliées par a.

Exemple : ^a = 105°, ^b = 45°. La somme des angles égalant 180°, on a ^c = 30°. On pose a =1, la formule des sinus s'écrit 1/sin105° = b/sin45° = c/sin30°. D'où b = sin45°/sin105° ≅ 0,732; c = sin30°/sin105° ≅ 0,518. Si la mesure de a est 23 m, alors b = AC = 23 × 0,732 ≅ 16,84 m, c = AB = 23 × 0,518 ≅ 11,91 m.

Programme Javascript :

Pour le "confort" de l'utilisateur, l'ordinateur considérera 8 cas : dans l'étude et dans le programme qui en résultera, le sommet A sera toujours l'angle "au sommet" et B "à gauche" de C. Si un seul côté (resp. angle) est connu, le programme supposera qu'il s'agit de a = BC (resp. ^a = ^BAC). Ainsi, le programme proposé évitera à l'utilisateur des tortures intellectuelles du type retournement (échange de B et C par exemple). Ce dernier pourra identifier son triangle en se limitant à une simple rotation (permutation circulaire) et à une correspondance biunivoque entre A, B, C et les appellations de ses propres sommets.

         
 

© Serge Mehl - www.chronomath.com