ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 HURWITZ Adolf,
allemand, 1859-1919 |
!
Ne pas confondre ce mathématicien
allemand avec le mathématicien polonais Witold
Hurewicz (1904-1956).
Adolf Hurwitz étudia à Munich, Berlin et Leipzig où il obtint son doctorat dirigé par Klein, portant sur les fonctions modulaires (1881).
Il fut professeur en les célèbres universités de Göttingen, de Königsberg (Kaliningrad) où il connut Hilbert, et à l'École polytechnique de Zurich (1892) qui hébergèrent les plus grands mathématiciens allemands avant l'apparition du nazisme.
Les travaux d'Hurwitz furent influencés par ceux de son maître Felix Klein. Il s'intéressa ainsi principalement aux structures algébriques fondamentales, à la théorie des courbes algébriques, aux fonctions elliptiques et modulaires qu'il appliqua à la théorie des nombres algébriques eu égard aux travaux de Kronecker.
|
Quaternions d'Hurwitz (1919) : |
Lorsque les composantes a, b, c et d d'un quaternion d'Hamilton a + bi + cj + dk sont choisies dans l'anneau Z des entiers relatifs, on parle de quaternions de Lipschitz et on obtient non plus un corps mais un anneau. Plus généralement :
On appelle quaternion d'Hurwitz un quaternion dont les quatre composantes sont soit dans Z soit dans ½ + Z, pour signifier les nombres de la forme ½ + n, n∈Z. Ils constituent un anneau euclidien (donc factoriel).
Tout quaternion d'Hurwitz peut aussi s'écrire sous la forme a(1 + i + j + k)/2 + bi + cj + dk.
On trouvera en réf.5 une jolie preuve du théorème des 4 carrés de Lagrange au moyen des quaternions d'Hurwitz.
Hamilton et les quaternions : » Quaternions de Lipschitz : »
|
Un théorème d'Hurwitz (approximation diophantienne, 1891) : |
Si x est un irrationnel positif, il existe une infinité d'approximations rationnelles de x de la forme a/b telles que :
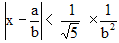
et si x est distinct du nombre d'or Φ, soit x ≠ (1 + √5)/2, et de ses composés élémentaires dans Q(Φ) la majoration devient :
Ce résultat complète celui de Legendre relatif à l'approximation d'un nombre irrationnel par une fraction continue. Dans le cas du développement de x en fraction continue, les réduites an/bn vérifient cette inégalité qui permet d'arrêter le développement avec toute la précision voulue.
➔ Pour en savoir plus :
ABRÉGÉ D'HISTOIRE DES MATHÉMATIQUES, 1700-1900
Ch VIII, Approximations diophantiennes par W. et F. Ellison, Ed. Hermann, Paris - 1992
Histoire d'algorithmes : Du caillou à la puce
(IREM,
IUFM, CNRS) -
Éd. Belin - Collection Regards sur la science - 1993.
Arithmétique et théorie des nombres, par Jean Itard, Que Sais-je n°1093, Ed. P.U.F., Paris.
Construction de nombres transcendants par Maurice
Mignotte (Faculté des sciences d'Orsay, 1973).
http://portail.mathdoc.fr/PMO/PDF/W_WALDSCHMIDT-169_3.pdf
Arithmétique, quaternions et quaternions d'Hurwitz,
par W. Stein, Univ. Washington :
http://modular.math.washington.edu/edu/2010/414/projects/hoon_kwon.pdf
Pick