ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 PICK Georg Alexander,
autrichien, 1859-1942 |
Georg Pick fit ses études à Vienne et enseigna les mathématiques à l'université de Prague. Victime du régime nazi, il mourut en déportation à Theresienstadt (aujourd'hui Terezin en République tchèque). On lui doit une élégante formule calculant l'aire de polygones tracés sur un quadrillage :
| Formule (ou théorème) de Pick : |
L'aire d'un polygone dont les sommets sont les nœuds d'un quadrillage est donnée par la formule :
A = s/2 + i - 1
où s désigne le nombre de sommets en question et i le nombre de nœuds strictement intérieurs au polygone.
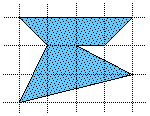
Dans l'exemple ci-dessus, l'aire est ainsi A = 5 + 3 - 1 = 7 (exprimée en carreaux), ce que l'on peut vérifier en écrivant A= 12 - A' où A' désigne la somme, aisément calculable, des aires des triangles que l'on dénombre entre le polygone et le rectangle 3 × 4 dans lequel il est inscrit.
➔ On pourra trouver la preuve détaillée et illustrée de ce résultat :
Morley