ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
BOMBIERI Enrico,
italien, 1940-
Médaille Fields 1974 |
Source Portrait
:
Ambassade d'Italie à Washington
Bombieri naquit à Milan. Il y fera ses études et obtiendra son doctorat portant sur la théorie algébrique des nombres à l'université de sa ville natale en 1963, sous la houlette de Giovanni Ricci (1904-1973), éminent spécialiste en la matière.
Bombieri fut professeur à l'université de Pise de 1966 à 1974, année où il reçoit (avec Mumford) la médaille Fields, lors du Congrès international de mathématiques de Vancouver, en reconnaissance de ses travaux en théorie des nombres.
En 1977, la chaire
IBM-Von Neumann (chaire honorifique en l'honneur de
John von Neumann qui fut
professeur à Princeton et ingénieur chez IBM jusqu'à sa mort en 1957) lui est proposée
au sein du célèbre Institut of Advanced Study de Princeton.
Bombieri reçut également le prix Balzan en 1980 et, plus récemment (mars 2010), le prix roi Fayçal d'Arabie pour les mathématiques, partagé avec le jeune mathématicien australien Terence Tao.
Les travaux de Bombieri portent également sur la théorie des fonctions de plusieurs variables complexes, les équations aux dérivées partielles, les variétés différentielles, surfaces minimales, ...
|
Théorème de Bombieri-Davenport (1966) : |
Dans le même cadre de recherches que ci-dessus, Bombieri et Davenport apportèrent un beau résultat relatif à la distribution des nombres premiers, s'exprimant très simplement, et s'avérant une avancée significative pour la preuve de l'infinitude des nombres premiers jumeaux :
Si on note pn le n-ème nombre
premier, il existe une infinité d'entiers n pour lesquels
pn+1 - pn <
½ln pn (ln
désignant le logarithme népérien)
» Dirichlet , Brun , Tao , Green , Zhang
|
Théorème de Bombieri-Vinogradov (1965) : |
Depuis Euler, Gauss et Riemann, les recherches sur la distribution des nombres premiers approximations relèvent d'une difficile théorie analytique des nombres (immixtion de l'analyse réelle et complexe dans l'arithmétique) et requièrent, pour une large part, l'hypothèse de Riemann sur les zéros de la fonctions ζ (zêta) prolongée à C.
Concernant π(x,a,b) mesurant le nombre de nombres premiers p inférieurs à x de la forme p ≡ a [b], les résultats de Dirichlet sur l'existence et la distribution de progressions arithmétiques de nombres premiers, permettent de conjecturer :
π(x,a,b) ~ π(x)/φ(b)
ou encore, puisque π(x) ~ x/ln x :
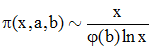
Dans le calcul de la majoration de l'erreur commise par cette approximation, Bombieri et le russe A.I. Vinogradov établirent indépendamment (1965/66) l'important résultat ci-dessous permettant de contourner la célèbre hypothèse. Les formulations sont multiples et variées; voici celle de G. Tenenbaum & M. Mendès-France (» réf. 4) :
On note :
• π(x) le nombre de nombres premiers
inférieurs à x (»
théorème des
nombres premiers);
• π(x,a,b), le nombre de nombres premiers inférieurs à
x de la forme a + nb, soit : Card{p∈N,
p premier, p ≤ x, p
≡ a [b]};
• φ(b) =
Card{k, k∈N,
1 ≤ k ≤ b - 1, pgcd(k,b) = 1} (» fonction indicatrice d'Euler);
• E(x,a,b) = Max3≤ y ≤ x
|π(y,a,b) - π(y)/φ(b)|.
alors :
Pour tout A > 0, x ≥ 3 et Q ≥ 1 on a :
avec a∧b = pgcd(a,b), O : notation de Landau
i Il s'agit ici de Askold Ivanovitch Vinogradov (1929-2005), mathématicien et physicien russe, spécialiste en théorie analytique des nombres, et non de son compatriote Ivan MatveïevitchVinogradov (1891-1983).
Le terme Q√x(lnQx)4 de cette majoration est peu satisfaisant si x est "grand" et par là également Q, borne supérieure des modulos (raisons des progressions). Trois ans plus tard les mathématiciens D. T. A. Elliott et Heini Halberstam apportent une correction, mais il ne s"agit là que d'une conjecture :
Conjecture de Elliott-Halberstam :
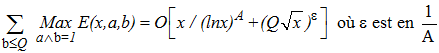
i Peter D. T. A. Elliott (1941-), mathématicien américain dont les recherches portent sur la théorie analytique des nombres. Il soutint sa thèse de doctorat, dirigée par Davenport (Some problems in analysis number theory, 1966), à l'université de Cambridge (Angleterre). Professeur à l'université du Colorado Boulder.
i Heini Halberstam (1926-2014), mathématicien anglais d'origine tchèque dont les recherches portèrent sur la théorie analytique des nombres. Il soutint sa thèse à l'université de Londres (Some results in analysis number theory, 1952), dirigée par Theodor Estermann. Professeur au Trinity College de Dublin puis à l'université de Nottingham, il termina sa carrière aux Etats-Unis à l'université de l'Illinois (source Wikipedia en).
➔ On pourra consulter en ligne le mémoire d'Alisa Sedunova (univ. Californie) étudiant la conjecture de Bombieri au moyen des fonctions Ψ de Tchébychev et Λ de von Mangoldt (» réf.7).
Les fonctions Λ de von Mangoldt et Ψ de Tchébychev : »
Le prix Fayçal :
En 1976, année suivant la mort du roi
d'Arabie, Fayçal ben Abdelaziz al Saoud (1904-1975), ses fils fondent The King Faisal foundation (Fondation du roi Fayçal). Elle
récompense annuellement (200 000 $US en 2010) les hommes et les femmes pour leurs contribution
exceptionnelle dans les domaines de la religion musulmane, de la langue et
littérature arabes et de la recherche
scientifique et médicale.
➔ Pour en savoir plus :
Prix du roi Fayçal (The King Faisal foundation) : http://www.kff.com/en/King-Faisal-International-Prize
Prix Balzan : http://www.balzan.org/fr/laureats/enrico-bombieri
Répartition des nombres premiers par J.-L.
Nicolas, Séminaire Delange-Pisot-Poitou :
http://archive.numdam.org/article/SDPP_1967-1968__9_2_A12_0.pdf
Les nombres premiers
The bombieri-vinogradov theorem, par R. C. Vaughan :
http://www.personal.psu.edu/rcv4/Bombieri.pdf
Théorie analytique des nombres,
par Michel Waldschmidt (univ. Paris VI), 2008 :
http://www.math.jussieu.fr/~miw/articles/pdf/TdN2008fasc8.pdf
Dhombres