
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges


! On ne le confondra avec le mathématicien allemand Felix Bernstein, encore moins avec le chef d'orchestre américain Leonard Bernstein (1918-1990)...
Né à Odessa (en Ukraine, au bord de la mer Noire), Serge Bernstein étudia à Göttingen et à Paris où il présenta (1904) une thèse intitulée Sur la nature analytique des solutions des équations aux dérivées partielles du second ordre obtenant un premier doctorat dont le jury comprenait Hilbert et Picard. Bernstein ne s'en tint pas là : rentré à Kharkov (Ukraine) en 1907, il obtient un poste d'enseignant et un second doctorat en 1913.
En 1933, Serge Bernstein enseigna ensuite à Leningrad (qui reprit son nom impérial, Saint-Pétersbourg, en 1991) et à l'Institut Steklov de mathématiques de Moscou, dès 1943.
Dans le prolongement de sa première thèse, ses travaux portèrent sur les équations aux dérivées partielles (il donnera une réponse partielle au 19è problème de Hilbert), puis le calcul des probabilités et son application à la génétique avec un essai d'axiomatisation (1917) que finalisera Kolmogorov, l'analyse fonctionnelle et la recherche de la meilleure approximation des fonctions continues par des polynômes (polynômes de Bernstein) lesquels seront utilisés par Stone dans la démonstration de la forme généralisée du théorème dit de Stone-Weierstrass.
Admiratif des travaux de Tchebychev, il fut à Moscou l'éditeur de ses œuvres déjà publiées en russe et en français par Andreï A. Markov, illustre élève de ce dernier en 1899. On doit également à ce grand mathématicien (1908) une preuve partielle de la généralisation du problème de Dirichlet (20è problème de Hilbert).
Il s'intéressa également à la théorie différentielle des surfaces et plus particulièrement aux surfaces minimales (dont l'aire est minimale) en posant un problème portant aujourd'hui son nom qu'il résolut dans le cas de l'espace euclidien usuel (dimension 3) :
Théorème de Bernstein (1915) :
Une surface minimale de R3 d'équation z = f(x,y) où f admet des dérivées continues des premier et second ordre pour tout (x,y) se réduit à un plan; autrement dit z est une fonction affine de x et y.
Le problème fut de généraliser le résultat aux hypersurfaces de Rn en tant que variété différentielle de dimension n - 1 admettant une représentation sous la forme f(x1, ...,xn-1) = 0. De nombreux mathématiciens se penchent sur la question. En généralisant à Rn une condition d'Euler pour les surfaces minimales (» réf.7a & 7b) :
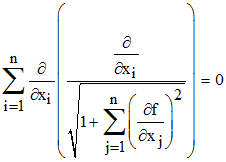
Bombieri, Ennio de Giorgi (1928-1966), professeur à Pise et Enrico Giusti (1940-), professeur à Florence, publient conjointement (Minimal cones and Bernstein problem,1969), un article selon lequel le théorème de Bernstein se généralise jusqu'à n = 8 mais non au-delà : dans les mêmes conditions de continuité, f(x1, ...,xn-1) est du premier degré en x1, ...,xn-1 et définit ainsi un hyperplan.
|
Polynômes de Bernstein : |
Ces polynômes constituent, d'une façon générale, une base (Bn) des polynômes d'une variable réelle de degré n et sont définis par :
|
On remarquera que si t est un réel de [0,1],
Bk(t) correspond à la
probabilité binomiale B(n,p) :
Bk(t) = Prob {Bn = k} On en déduit, dans ce cas, que
Σ Bk(t)
= 1 pour tout t de [0,1] » Ce résultat se retrouve également en développant [t + (1 - t)]n... |
∗∗∗
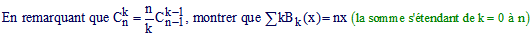
♦ Polynômes d'approximation de Bernstein :
Soit f une fonction continue sur l'intervalle [0,1]. La suite de polynômes Pn(f) définie par :
converge uniformément vers f sur l'intervalle [0,1]. C'est donc dire que pour tout ε > 0, il existe Nε tel que :
∀ n ≥ Nε , ∀ x ∈[0,1] , | f(x) - Pn(f)(x) | < ε
Par changement de variable affine, le résultat peut se prolonger à une fonction définie et continue sur un intervalle [a,b]. Ces polynômes apportent une preuve du théorème de Weierstrass (1885), également dit de Stone. A ce sujet, on pourra consulter avec profit les références 3 à 6 proposées in fine.
♦ Inégalité de Bernstein :
Sur l'intervalle [0,1] et plus généralement [-1,1], on peut remplacer la variable x par un cosinus ou un sinus (comme le fit Tchebychev). Bernstein établit (1912) cette inégalité :
Soit Pn le polynôme trigonométrique de la variable θ défini sur l'intervalle J = [0,2π] par :
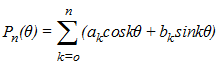
alors le polynôme dérivé P'n vérifie l'inégalité |P'n(θ)| ≤ n × MaxJ |Pn|
Preuve : » preuve donnée par Marcel Riesz en réf.4 ci-dessous.
➔ Pour en savoir plus :
Sur un théorème de géométrie et son application aux
dérivées partielles du type elliptique, par S. Bernstein (1915) :
http://www.mathnet.ru/links/81a8299eee4e94e2788509aba6820e8e/khmo15.pdf
Polynômes de Bernstein et applications, une
introduction en termes probabilistes, page de Daniel
Agier (académie de Grenoble) :
http://www.ac-grenoble.fr/disciplines/maths/pages/PM/Ressources/25/FicheProfesseurPolynomesDeBernstein.pdf
Polynômes de Bernstein : page de Jean-Louis Rouget sur les polynômes de Bernstein et leur application
au théorème ci-dessus :
http://www.maths-france.fr/MathSpe/GrandsClassiquesDeConcours/Polynomes/PolynomesBernstein.pdf
L'œuvre mathématique de Marcel Riescz, II, 1983 : http://www.numdam.org/article/CSHM_1983__4__1_0.pdf
Sur les polynômes d'approximations par Pierre Montel : http://www.numdam.org/article/BSMF_1918__46__151_1.pdf
Quelques aspects des surfaces minimales, par
Alexis Michelat et Sheng Yuan Zhao ENS) :
https://www.math.ens.fr/enseignement/telecharger_fichier.php?fichier=1432
a) Una estensione del teorema di Bernstein , par
Ennio de Giorgi (1965) :
http://www.numdam.org/article/ASNSP_1965_3_19_1_79_0.pdf
b) Régularité des hypersurfaces minimales, par Enrico Bombieri
(séminaire Bourbaki, 1968-69) :