ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

BÉZOUT (Bezout) Étienne, français, 1730-1783      » Identité de Bézout

Natif de Nemours, professeur de mathématiques auprès des gardes de la Marine et de l'École d'artillerie (Monge lui succédera en 1783), Étienne Bézout (ou Bezout, comme très souvent dit et écrit de nos jours) édita de nombreux manuels pédagogiques.

Bezout vécut à Avon, près de Fontainebleau en Seine & Marne. Sa statue, en marbre blanc de Carrare,  a été érigée en 1885 à sa mémoire, place de la République (Nemours) à la demande de la municipalité (1883), par le sculpteur français Justin C. Sanson (1833-1910), auteur de nombreuses œuvres ornant d'importants édifices comme le Louvre, l'Hôtel de ville de Paris, l'opéra Garnier (» réf.1).

Le Cours de mathématiques en 6 volumes d'Étienne Bézout, édité entre 1764 et 1769 eut une grande audience dans les écoles militaires, dont l'École de Brienne où étudia Bonaparte, ainsi qu'à l'École Polytechnique de Paris dès sa création en 1794. Traduit en anglais, son influence s'élargit jusqu'aux Etats-Unis d'Amérique dans l'enseignement des mathématiques au 19è siècle.

Ses recherches sur la rectification des courbes planes et leurs intersections lui valurent d'entrer à 28 ans (!) à l'Académie des sciences (1758). Mais le record n'est pas battu : son contemporain d'Alembert, mort la même année que lui, y entra en 1741 à l'âge de 24 ans...

Son nom est principalement attaché à ses travaux sur les équations algébriques et à un célèbre résultat qu'il établit dans son traité de 1779 sur la divisibilité des polynômes, étudié en classe terminale S SpéMath dans le cadre de l'arithmétique sous l'appellation identité de Bezout. Ses travaux seront en partie complétés par l'algébriste anglais James Sylvester.

Travaux sur les équations algébriques et les polynômes :

Son œuvre principale sera sa Théorie générale des équations algébriques (1779) où il développe sa méthode d'élimination consistant, face à deux équations algébriques f(x) = 0 et g(x) = 0 à rechercher la condition pour laquelle elles admettent au moins une racine commune.

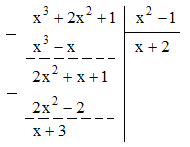Ces travaux amènent Bezout à l'algorithme de division des polynômes très proche, dans la démarche, à celle des entiers naturels : deux polynômes A et B étant donnés, il existe un unique polynôme Q et un unique polynôme R de degré strictement inférieur à B tel que A = B × Q + R, c'est à dire que pour tout x : A(x) = B(x) × Q(x) + R(x).

On parle là encore de division euclidienne de A par B. Q est le quotient et R le reste. Et on peut poser une division comme dans les entiers naturels. Dans l'exemple ci-contre, on peut écrire :

x3 + 2x2 + 1 = (x2 - 1)(x + 2) + x + 3

Si le polynôme R est nul, on dit que B divise A.

Division de polynômes par la méthode de Horner : »

 ➔  Deux polynômes A et B sont dits premiers entre eux si leurs seuls diviseurs communs sont des scalaires (nombres considérés comme polynômes de degré 0. Bézout montre alors le résultat suivant :

♦  Pour que les polynômes U et V soient premiers entre eux il faut et il suffit qu'il existe deux polynômes A et B tels que A x U + B× V soit identiquement égal à l'unité.

Cela revient à énoncer :

♦  Pour que les polynômes U et V n'admettent aucune racine commune, il faut et il suffit qu'il existe deux polynômes A et B tels que A × U + B × V soit identiquement égal à l'unité.

Un théorème de Bézout (1764) relatif aux courbes algébriques :     

Deux courbes algébriques de degré n et p se rencontrent en au plus n x p points, à moins que leurs équations,
de la forme f(x,y) = 0 et g(x,y) = 0, aient un facteur commun non trivial.

Prouvé par Bézout dans le cas où les points communs sont simples (sur chaque courbe) avec des tangentes distinctes, ce résultat fut partiellement démontré auparavant par Maclaurin. Plus tôt encore, Newton l'affirma sans démonstration dans les mêmes hypothèses (Arithmetica universalis, 1707).  Euler s'y attaqua en 1748 (» réf.2) et Cramer en 1750 tout en y trouvant à redire... :

Paradoxe de Cramer : »             » Plücker , Clebsch

En particulier : 

Une conique et une cubique non dégénérées se coupent en 6 points au plus

Par conique non dégénérée, on entend une conique non réduite à un point ou une droite et par cubique non dégénérée, une cubique dont l'équation algébrique est donnée par un polynôme irréductible du 3ème degré en x et y. On pourra consulter la preuve de ce résultat donnée par Jérôme Germoni (univ. Lyon1, » réf.3, page 15).

∗∗∗
En admettant qu'une cubique puisse être définie par un polynôme réductible, montrer qu'une telle courbe peut contenir une conique. ☼

Sections coniques d'Apollonius : »            Wallis et les coniques en tant que courbes algébriques de degré 2 : »

Identité de Bézout, au + bv = 1 :

Également dit théorème de Bachet de Méziriac, cette célèbre identité (du monde mathématique) est liée aux travaux précédents :

Pour que les entiers naturels u et v soient premiers entre eux, il faut et il suffit qu'il existe
deux entiers relatifs a et b tels que au + bv = 1.

Par exemple :  

Ce résultat, permet de résoudre les équations diophantiennes de la forme ax + by = c   (où a, b et c sont entiers).

Algorithme et résolution de l'équation ax + by = c sur ordinateur : »

∗∗∗

1.  a)  En utilisant l'algorithme d'Euclide, calculer le PGCD de 3046 et 45.
En déduire une solution de l'équation 3046x - 45y = 5  ☼
2.  Paul, alors enfant, né au 20è siècle, avait calculé qu'en l'an 2000, son âge serait égal à la somme des chiffres de son année de naissance.
 En quelle année est-il né ? (Bac C, Abidjan juin 1989)  ☼        3.  Auberge d'Euler
 

 ➔  Pour en savoir plus :

  1. Etienne Bézout sur le site Mathouriste d'Alain Jouhel : http://home.nordnet.fr/~ajuhel/Bezout/Bezout.html.

  2. Analyse algébrique au siècle des Lumières , par Lilianne Alfonsi : https://arxiv.org/pdf/0910.3641.pdf

  3. Cours sur les coniques de Jérome Germoni (univ. Lyon1) : http://math.univ-lyon1.fr/~germoni/agreg/coniques.pdf

Bougainville  Malfatti
© Serge Mehl - www.chronomath.com