ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

BERGE Claude, français, 1926-2002

» photographie  : Source INRIA (voir aussi en compagnie de Paul Erdös ,1995).

Mathématicien éclectique, Claude Berge, décédé le 30 juin 2002, fut aussi un homme de lettres et un sculpteur reconnu. Chercheur au Centre d'Analyse et de Mathématique Sociales (CAMS), rattaché au Centre National de la Recherche Scientifique (CNRS), il fut directeur de l'UER en combinatoire.

Ses travaux en théorie des graphes lui ont valu une réputation internationale. On lui doit en particulier la Théorie générale des jeux à n personnes (1957) et, l'année suivante, la Théorie des graphes et ses applications.

En littérature, Berge est à l'origine, avec Georges Perec, Raymond Queneau et François le Lionnais, de l'Oulipo = Ouvroir de littérature potentielle conciliant littérature et mathématique dans la recherche d'une productivité littéraire soumise à des contraintes formelles.

Dès le début des années 1960, Berge sera à l'origine, avec la collaboration de grands champions, dont F. Le Lionnais, de la programmation de "machines" à jouer aux échecs. Sa notoriété lui vaudra de nombreuses chaires d'enseignement dont la Sorbonne (Paris I), l'université Pierre & Marie Curie (Paris VI), Princeton (USA), Pékin, Bombay.

» Von Neumann , De Possel        

Recherche opérationnelle et théorie des graphes :

Les travaux de Berge portèrent sur essentiellement sur la recherche opérationnelle (théorie des jeux), l'analyse combinatoire et la théorie des graphes qu'il développa au plus haut niveau et dont Euler fut l'initiateur avec le célèbre problème des sept ponts de Königsberg (» ci-dessous).

Les applications de la théorie des graphes sont immenses tant au plan civil que militaire  : aide à la décision, stratégie, optimisation (plus court chemin, GPS), réseaux de transports (chemins de fer, lignes aériennes), réseau d'électricité, ports et aéroports, ordonnancement des tâches. La théorie des graphes n'est pas une branche indépendante des mathématiques, elle se rattache à la programmation linéaire, la programmation convexe (où le concept plus général de fonction convexe remplace les fonctions linéaires et affines), la topologie, le calcul des probabilités.

Contemporains de Berge, R. Faure et A. Kaufmann en France, F. Harary, Ford Lester Randolph Jr. aux États-Unis, le polonais Kuratowski et le hongrois Erdös, sont également considérés comme les leaders du développement de la théorie des graphes et de ses applications au 20è siècle.

Notion de recherche opérationnelle : »             Le théorème des 4 couleurs : »

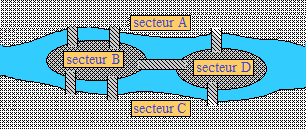
Problème des sept ponts de Königsberg :       

Partant d'un point de la ville, peut-on se promener, en revenant à son point de départ, en passant une seule fois par tous les ponts ?

           
»  Université de Königsberg (Kaliningrad, Fédération de Russie)

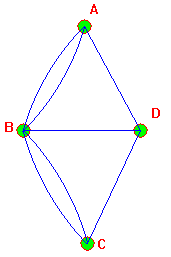
Euler résolut ce problème (1735) en le modélisant par un graphe (à droite) : les 7 arcs (courbes ou linéaires) symbolisent les ponts reliant les différents quartiers de la ville (nord, sud, île ouest, île est) : les sommets du graphe.

Ce graphe est non orienté : les arcs peuvent être parcourus dans les deux sens. Il est également connexe : on peut aller d'un sommet à n'importe quel autre (en suivant un ou plusieurs arcs). Si l'on peut aller d'un sommet à un autre en ne parcourant pas deux fois un même arc, on dit que la suite d'arcs parcourus est un chemin. On dit qu'un chemin est fermé, si le sommet de départ et d'arrivée coïncident.

Graphe eulérien :      

Il s'agit d'un graphe connexe que l'on peut parcourir entièrement en suivant un chemin fermé (au sens ci-dessus). Eulerprouva que tout sommet d'un graphe de ce type doit être relié à un nombre pair d'arcs.

Il s'agit donc ici se savoir si le graphe des 7 ponts réalise un chemin fermé. Le graphe correspondant à la situation est dessiné à droite. La réponse au problème est donc non.

Promenade virtuelle (site externe de Jean-Marc Deleuze) : http://rigolmath.free.fr/ponts/ponts.htm

La théorie des graphes relève de ce qu'on a appelé la topologie combinatoire dans les années 1920-1940. L'immixtion de l'algèbre (morphisme, théorie des groupes) par Emmy Noether et Hopf a conduit à la topologie algébrique.

Topologie combinatoire et algébrique : »             En savoir  plus sur la théorie des graphes : »

 ∗∗∗ 
niveau Ter ES : »         niveau Sup : »

 ➔  Pour en savoir plus :

            

Tate  Cooley
© Serge Mehl - www.chronomath.com