ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 FORD Lester Randolph
Henry Sr. , américain, 1886-1975 |
Ce mathématicien, diplômé de l'université de Harward (1917), fut un spécialiste en théorie de nombres (approximations rationnelles dans le champ réel et complexe) et en analyse fonctionnelle.
i Le fils de Ford, Ford Lester Randolph Jr., né en 1927, est également mathématicien et spécialiste en recherche opérationnelle et théorie des graphes; son nom est attaché à l'algorithme de Ford-Fulkerson, un outil s'appliquant en particulier dans les problèmes d'optimisation des réseaux de transport. On pourra consulter un exemple "pédagogique" sur Images des mathématiques (CNRS/IHP).
Ford fut président de l'Association américaine de mathématiques (MAA) en 1947-48. Cette dernière créa, en son honneur (1964), un prix portant son nom et récompensant des mathématiciens du monde entier pour leurs contributions en mathématiques auprès de la MAA (épistémologie ou travaux). Jean Dieudonné fit partie des récipiendaires en 1971 pour sa publication The work of Nicholas Bourbaki (1970).
| Cercles de Ford : |
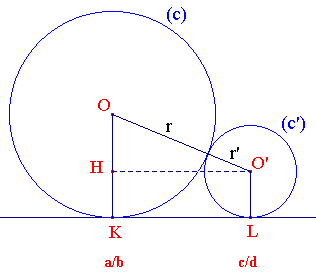
Ford donna une interprétation géométrique de la curieuse propriété des suites (finies) de fractions découvertes par Farey en étudiant une famille de cercles tangents :
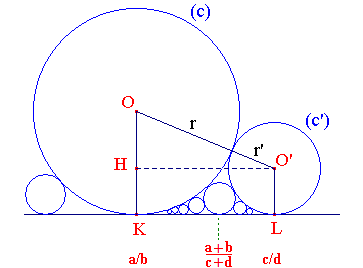
Étant donné un axe gradué et deux cercles de centres respectifs O et O', de rayons respectifs r et r' (r' < r) tangents à l'axe en K et L, cherchons la condition sur KL pour qu'ils soient tangents extérieurement. On note x = a/b et x' = c/d les abscisses rationnelles de K et L.
L'application du théorème de Pythagore conduit à :
(r - r')2 + (x' - x)2 = (r + r')2
donc à : 4rr' = (x' - x)2. Notons d et d' les diamètres respectifs des cercles. On a :
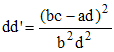
En particulier, si ad - bc = 1 , d = 1/b2 , d' = 1/d2, avec d > b, alors les cercles sont tangents extérieurement et à l'axe. On remarque que la condition ad - bc s'écrit :
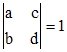
On a donc aussi (propriété des déterminants) mais on peut le vérifier par le calcul direct de (a + c)d - (b + d)c et a(b + d) - b(a + c) :
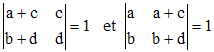
Par suite, le cercle d'abscisse
, de diamètre
est tangent
extérieurement aux cercles (c) et (c') ainsi qu'à l'axe. On retrouve la
propriété d'insertion des suites de fractions de Farey.
Ce résultat peut être illustré par la suite
et les cas a/b
= 1/2 et c/d = 2/3.
La figure ci-dessous évoque le processus récurrent de construction :
Par symétrie et un calcul analogue on obtiendra une interprétation d'un cas comme a/b = 1/5 et c/d = 1/3 : le cercle (c') de rayon plus petit serait à gauche de (c). On peut également s'intéresser à des fractions supérieures à 1, voire aux entiers.
➔ Des sphères peuvent remplacer les cercles. Les résultats s'avèrent très esthétiques et ont un aspect fractal :
Lévy