ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Podaire du deltoïde              » les hypocycloïdes , étude analytique , podaire (cas général)

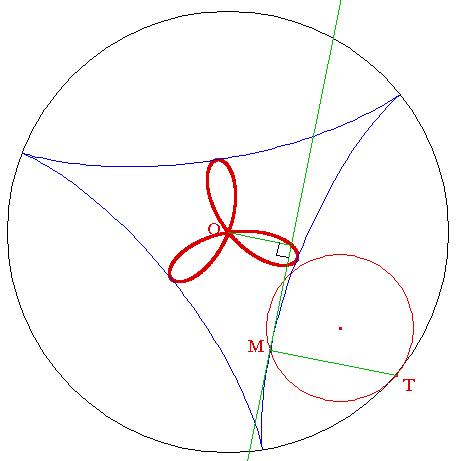
Le deltoïde (en forme de delta) est obtenu comme lieu d'un point M d'un cercle de rayon r roulant sans glisser à l'intérieur d'un cercle de rayon 3r. On pourra consulter cette animation CabriJava :

•••  Génération du deltoïde : »

Il s'agit ici de rechercher l'ensemble des pieds H des perpendiculaires aux tangentes au deltoïde issues de l'origine. La figure et les notations sont celles de la génération du deltoïde rappelée ci-dessus.

À chaque instant, la normale à la courbe est portée par (TM). Il est donc aisé de construire la tangente en M puis la perpendiculaire. On obtient un superbe trifolium dont voici l'animation Cabrijava :

Si votre navigateur accepte les applets Java (» extension CheerpJ) :
Pour effacer / relancer le lieu : double-cliquer / cliquer dans la figure. Vous pouvez aussi déplacer T manuellement.