Podaire du deltoïde

ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Trifolium en tant que podaire du deltoïde ••• animation
» Trifolium (étude polaire directe) , deltoïde

Le deltoïde a pour équation paramétrique :

x = 2cos t + cos 2t , y = 2sin t - sin 2t (r = 1, R = 3)

Selon la théorie, l'équation de la podaire par rapport à O sera :cos(t)-

X = y' x (xy' - yx')/(x'² + y'²) , Y = x' x (yx' - xy')/(x'² + y'²)

ce qui conduit sans difficultés aux relations x'² + y'² = 8 - 8cos 3t et xy' - yx' = 2 - 2cos 3t. D'où l'équation de la podaire, trifolium et sa courbe représentée ci-dessous en bleu :

X = (cost - cos2t)/2 , Y = (sint + sin2t)/2 , t variant sur [0,2π] ou [-π,+π]

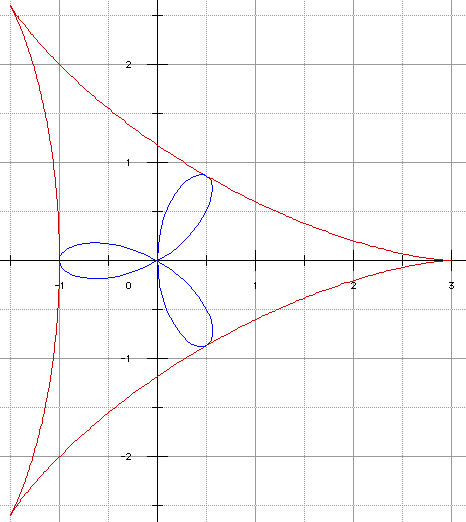
➔ Mais le trifolium est plutôt connu par son équation polaire :

r = acos3t , t variant de 0 à π

ce qui équivaut, en coordonnées paramétriques à :

x = acos3t.cost et y = acos3t.sint

Les formules de transformation de produits en sommes fournissent (avec a = 1/2) :

x = (cos4t + cos2t)/2 et y = (sin4t - sin2t)/2

Posons t = u/2 :

x = (cos2u + cosu)/2 et y = (sin2u - sinu)/2 , u variant sur [0,2π]

Posons u = π + T :

x = (cos2T - cosT)/2 et y = (sin2T + sinT)/2 , T variant sur [-π,+π]

Effectuons la symétrie orthogonale d'axe Oy (cette isométrie conserve la nature de la courbe) : on change x en - x :

x = (cosT - cos2T)/2 et y = (sin2T + sinT)/2 , T variant sur [-π,+π]

C'est bien notre podaire.