ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 
Le deltoïde en tant qu'hypocycloïde
•••
animation
»
podaire du deltoïde
, cas de l'astroïde |
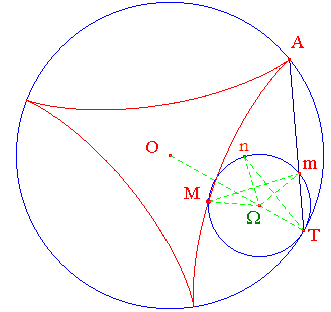
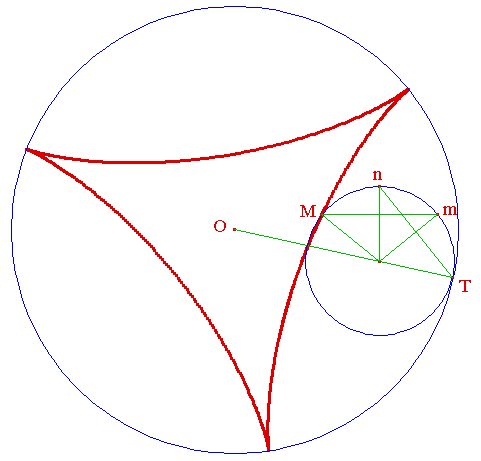
Le deltoïde (mot à mot : en forme de delta) est une hypocycloïde : il s'obtient comme lieu d'un point M d'un cercle de rayon r roulant sans glisser à l'intérieur d'un cercle de rayon R = 3r.
Au départ le cercle (c) est tangent (intérieurement) à (C) en A et le point M est en A.
À chaque instant, on note T le point de contact de (c) et (C).
Traçons [TA] qui coupe (c) en m.
L'homothétie de centre T qui transforme Ω en O (de rapport R/r), transforme (c) en (C) et m en A.
L'arc TA mesure donc 3 fois l'arc Tm.
Dire que le cercle (c) roule sans glisser signifie, en termes de longueur d'arc, que TM = TA.
À chaque instant, M est obtenu à partir
de m par deux symétries successives :
On obtient tout d'abord N, symétrique de T par rapport à (Ωm),
puis M, symétrique de m par rapport à (ΩN).
|
)
: