
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|
Dans toute la suite si (un) désigne une suite numérique, E(un) désignera la partie entière par défaut de un et sa partie fractionnaire (partie décimale illimitée ou non), c'est à dire {un} = un - E(un). La suite des {un} est à valeurs dans [0,1[. Au sens des congruences, on a {un} ≡ un [1], raison pour laquelle on parle de répartition modulo 1 des un.
La notion de répartition modulo 1 : »
Équirépartition :
Posons I = [0,1] et soit J = [a,b] un intervalle quelconque de I. A la manière du totient d'Euler, soit :
φ(n) = Card {k∈N, 1 ≤ k ≤ n, a ≤ {un}≤ b }
La suite {un} est dite équirépartie modulo 1 si elle est dense dans I et si, pour tout J, la suite φ(n)/n converge vers b - a.
Intuitivement, pour n suffisamment "grand", on doit avoir φ(n) ≅ n(b - a) pour tout J de I de longueur b - a : le nombre de {un} est "proportionnel" à n et à l'amplitude de l'intervalle J.
• L'ensemble des multiples nα d'un nombre réel α est équiréparti modulo 1si et seulement si α est irrationnel.
• Selon un résultat de J. F. Koksma (1933), la suite (αxn), pour α réel, est équirépartie modulo 1 pour presque tout réel x > 1, c'est à dire que l'ensemble des x > 1 tels que la suite n'est pas équirépartie est de mesure nulle au sens de Lebesgue. Mais selon Marcel David (Encyclopædia Universalis, Approximations diophantiennes, §6 répartition modulo 1), aucun x n'a encore été exhibé : un cas comme α = 1, x = 3/2 est un problème ouvert.
i J. Ferdinand Koksma (1904-1964), mathématicien hollandais. Spécialiste en théorie des nombres et approximations diophantiennes.
• Le cas des nombres de Pisot est un contre-exemple du théorème de Koksma : ils sont très mal répartis. Prenons le cas du nombre d'or Φ, c'est un nombre de Pisot. On constate dans le tableau de valeurs ci-contre que Φn prend des valeurs de "plus en plus entières" :
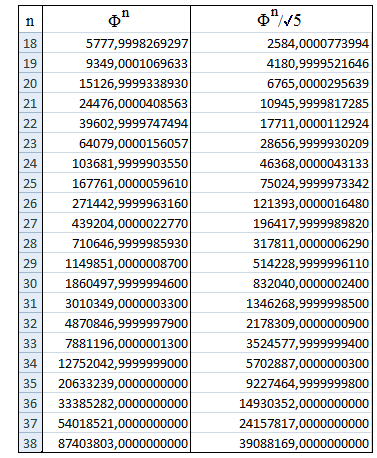
On peut prouver ce résultat dans ce petit exercice où il apparaît que la suite de terme général :
wn = Φn + (-1/Φ)n
ne prend que des valeurs entières (*). Lorsque n devient infini, vu que Φ = (1 + √5)/2 > 1, (-1/Φ)n tend ("très vite") vers 0. C'est dire que lorsque n tend vers l'infini, (Φ)n tend vers des valeurs entières. Pour n "grand" il y a alors accumulation des {Φn} au voisinage de 0 ou 1 : leur suite n'est pas dense dans [0,1] et la condition sur la limite de φ(n)/n n'est pas non plus vérifiée !
Il en est de même de la suite de terme général Φn/√5. En effet, selon la formule de Binet, le terme général de la suite de Fibonacci peut s'écrire :
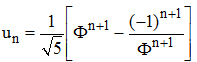
C'est à dire un = wn+1/√5. On obtient les mêmes conclusions en usant du même raisonnement.
(*) C'est un cas particulier d'un résultat général. On pourra consulter les deux références ci-dessous sur l'équirépartition modulo 1 :
➔ Pour en savoir plus :
La
répartition modulo 1 et les nombres algébriques, par Charles Pisot, 1938
:
http://archive.numdam.org/article/ASNSP_1938_2_7_3-4_205_0.pdf
Équirépartition modulo 1 d'après Hermann Weyl,
par Pierre de la Harpe (Univ. Genève) :
http://www.unige.ch/math/folks/delaharpe/vulgarisation/4Therg20mar05.pdf
De l'équirépartition modulo 1 aux nombres de Salem,
par E. H. El Abdalaoui et G. Grancher :
http://lmrs.univ-rouen.fr/Salem/nbressalem.pdf