
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
|
|

|
|
➔ Dire que θ est un entier algébrique signifie que θ est un zéro d'un polynôme minimal P, de variable complexe z à coefficients entiers, de trace et norme entières avec, dans ce cas d'étude, le coefficient du terme de plus haut degré égal à ±1, le terme constant ao est non nul et, quitte à changer P en -P, on peut supposer ao > 0 :
P(z) = εzn + an-1zn-1 + an-2zn-2 + ... + a2z2 + a1z + ao, ε = ±1, ao > 0
Le produit des racines est ici p = (-1)nao et ao entier assure | p | ≥ 1. Si on excepte le cas particulier où tous les zéros de P réels ou complexes sont de module 1, il existe au moins un zéro θ de P dont le module est strictement supérieur à 1, sinon | p | ≤ 1 et vu que| p | ≥ 1 on aurait | p | = 1 ce qui est écarté.
Pisot s'intéresse aux polynômes P admettant un unique tel θ, tous ses autres zéros étant intérieurs au cercle unité. Ce θ est un zéro réel : si tel n'était pas le cas, les coefficients de P étant entiers, il admettrait θ, conjugué de θ comme second zéro de module strictement supérieur à 1. Quitte à changer z en - z, on peut supposer θ > 0, donc θ > 1. Pisot appelle S l'ensemble de tels réels θ, S comme Raphaël Salem qui s'y intéressa au début des années 1940.
Exemples de nombres de Pisot :
Tout nombre réel z > 1, cas trivial...
Considérons l'équation x3 - x - 1 = 0 dont l'unique solution réelle est le nombre plastique Ψ ≅ 1,3247. On montre à la page suite de Padovan que les deux autres racines du polynôme x3 - x - 1, polynôme minimal de Ψ, sont de modules inférieurs à 1. Le nombre Ψ est le plus petit nombre de Pisot, preuve apportée par Siegel : Algbraic numbers whose conjugates lie in the unit circle, 1944 (» ref.2, accès retreint).
Le nombre d'or Φ ≅ 1,618, solution de x2 - x - 1 = 0, de conjugué 1 - Φ ≅ - 0,618 est un nombre de Pisot. Dans son mémoire cité ci-dessus, Siegel conjecture que Φ est le plus petit point d'accumulation de l'ensemble S des nombres de Pisot. Ce dernier prouve la conjecture en 1953 (» ref.1).
Extension algébrique d'un corps, polynôme minimal, conjugué d'un nombre algébrique : »
| Nombres de Salem : |
Dans ses travaux, Salem étudie ces nombres en élargissant leur définition à ρ ≤ 1. Si de tels nombres ne sont pas des nombres de Pisot, c'est à dire que un des conjugués (au moins) est de module 1, on parle alors de nombres de Salem notés σi ou τi suivant les auteurs et leur ensemble est généralement noté T.
➔ Le polynôme minimal P d'un nombre de Salem σ est réciproque. En effet, P (avec an= ε ±1) admet un zéro α de module 1 vérifiant donc P(α) = 0 et | α | = 1 = αα. On a alors Q(α) = αnP(1/α) = αnP(α) = αnP(α) = 0. Or P et Q ont le même degré et P est le polynôme minimal de α , d'où Q = P à une constante multiplicative près. En posant Q = kP, on a d'une part ao = kan = kε et an = kao. Donc k2 = 1. C'est dire que Q = ± P. En particulier si σ est un nombre de Salem, 1/σ annule le polynôme minimal de σ.
Salem prouva que tout nombre de Pisot est un point d'accumulation de T : en d'autres termes, on a S⊂T', c'est à dire que si θ est un nombre de Pisot, tout intervalle de centre θ contient un point de T. Par conséquent :
T est infini et ses éléments étant algébriques, cette infinité est dénombrable.
Tout nombre de Pisot est limite d'une suite de nombres de Salem.
Salem confirma (1944) une conjecture de Vijayaraghavan, selon laquelle l'ensemble S des nombres de Pisot est fermé dans R : Proof of a conjecture de Vijayaraghavan (» ref.3, accès restreint; voir aussi ref.5).
Point d'accumulation, ensemble dérivé, ensemble parfait : »
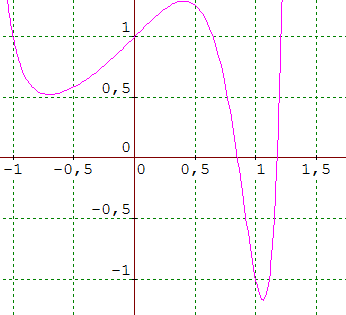
Le plus petit nombre de Salem découvert à ce jour est σ1 ≅ 1,1762808, son polynôme minimal est :
P(x) = x10 + x9 - x7 - x6 - x5 - x4 - x3 + x + 1
Il fut découvert par Derrick H. Lehmer en 1933. L'existence d'un plus petit élément de l'ensemble des nombres de Salem est un problème ouvert. Il en est de même de savoir si T est dense dans [1,+∞[.
En 1977, David W. Boyd exhiba 39 nombres de Salem inférieurs à 1,3. On en connaît aujourd'hui une cinquantaine (» ref.10 & 11).
Les nombres de Pisot trouvent leur intérêt dans l'étude des corps finis de nombres algébriques et s'avèrent utiles dans les approximations diophantiennes de nombres algébriques et dans les problèmes de convergence de suites trigonométriques (séries de Fourier, analyse harmonique), sujet de prédilection de Raphaël Salem.
➔ Pour en savoir plus :
Sur un ensemble fermé d'entiers algébriques (nombres
de Pisot ), 1953 :
http://archive.numdam.org/article/ASENS_1953_3_70_2_105_0.pdf
Algbraic numbers whose conjugates lie in the unit
circle, Siegel, 1944 (projet Euclide, accès limité) :
http://projecteuclid.org/DPubS?service=UI&version=1.0&verb=Display&handle=...
Proof of a conjecture de
Vijayaraghavan, Salem, 1944 (projet Euclide, accès
limité) :
http://projecteuclid.org/DPubS/Repository/1.0/Disseminate
view=body&id=pdffirstpage_1&handle=...
Pisot traite aussi les suites de
Farey
en liaison avec l'hypothèse de Riemann
:
http://archive.numdam.org/article/SDPP_1960-1961__2__A11_0.pdf
Distribution modulo 1 of the powers of real numbers
larger than 1, par Ch. Pisot et R. Salem :
http://archive.numdam.org/article/CM_1964__16__164_0.pdf
Sur les mauvaises répartitions modulo 1, par
Jean-Pierre Kahane (1964) :
http://archive.numdam.org/article/AIF_1964__14_2_519_0.pdf
Équirépartition modulo 1 d'après Hermann Weyl,
par Pierre de la Harpe (Univ. Genève) :
http://www.unige.ch/math/folks/delaharpe/vulgarisation/4Therg20mar05.pdf
De l'équirépartition modulo 1 aux nombres de Salem,
par E. H. El Abdalaoui et G. Grancher :
http://lmrs.univ-rouen.fr/Salem/nbressalem.pdf
Corps de nombres engendrés par un nombre de Salem,
par Frank Lalande (Université Paris 6, 1999) :
http://matwbn.icm.edu.pl/ksiazki/aa/aa88/aa8828.pdf
Nombres de Pisot inférieurs à Φ sur Wikipedia :http://fr.wikipedia.org/wiki/Nombre_de_Pisot-Vijayaraghavan
Petits nombres de Salem sur le site d'Eric Weisstein : http://mathworld.wolfram.com/SalemConstants.html
Petits nombres de Salem ordonnés par Lehmer : http://www.cecm.sfu.ca/~mjm/Lehmer/lists/SalemList.html